Question

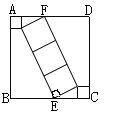
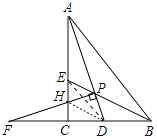
【题目】如图，Rt△ACB中，∠ACB＝90°，△ABC的角平分线AD、BE相交于点P，过P作PF⊥AD交BC的延长线于点F，交AC于点H，则下列结论：①∠APB＝135°；②PF＝PA；③AH+BD＝AB；④S四边形ABDE＝S△ABP，其中正确的是（　　）

A.①③B.①②④C.①②③D.②③

Answer 1

【答案】C

【解析】

根据三角形全等的判定和性质以及三角形内角和定理逐条分析判断．

在△ABC中，AD、BE分别平分∠BAC、∠ABC，

∵∠ACB＝90°，

∴∠A+∠B＝90°，

又∵AD、BE分别平分∠BAC、∠ABC，

∴∠BAD+∠ABE＝（∠A+∠B）＝45°，

∴∠APB＝135°，故①正确．

∴∠BPD＝45°，

又∵PF⊥AD，

∴∠FPB＝90°+45°＝135°，

∴∠APB＝∠FPB，

又∵∠ABP＝∠FBP，

BP＝BP，

∴△ABP≌△FBP，

∴∠BAP＝∠BFP，AB＝FB，PA＝PF，故②正确．

在△APH和△FPD中，

∵∠APH＝∠FPD＝90°，

∠PAH＝∠BAP＝∠BFP，

PA＝PF，

∴△APH≌△FPD，

∴AH＝FD，

又∵AB＝FB，

∴AB＝FD+BD＝AH+BD．故③正确．

连接HD，ED．

∵△ABP≌△FBP，△APH≌△FPD，

∴S△APB＝S△FPB，S△APH＝S△FPD，PH＝PD，

∵∠HPD＝90°，

∴∠HDP＝∠DHP＝45°＝∠BPD，

∴HD∥EP，

∴S△EPH＝S△EPD，

∵S四边形ABDE＝S△ABP+S△AEP+S△EPD+S△PBD

＝S△ABP+（S△AEP+S△EPH）+S△PBD

＝S△ABP+S△APH+S△PBD

＝S△ABP+S△FPD+S△PBD

＝S△ABP+S△FBP

＝2S△ABP，故④不正确．

故选：C．