题目内容
【题目】综合与探究
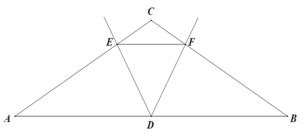
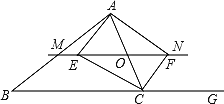
如图,等腰直角![]() 中,
中,![]() ,
,![]() ,现将该三角形放置在平面直角坐标系中,点
,现将该三角形放置在平面直角坐标系中,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() .
.
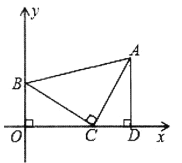
(1)过点![]() 作
作![]() 轴,求
轴,求![]() 的长及点
的长及点![]() 的坐标;
的坐标;
(2)连接![]() ,若
,若![]() 为坐标平面内异于点
为坐标平面内异于点![]() 的点,且以
的点,且以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,请直接写出满足条件的点
全等,请直接写出满足条件的点![]() 的坐标;
的坐标;
(3)已知![]() ,试探究在
,试探究在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形?若存在,请直接写出点
为腰的等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)4,![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)先根据![]() 证明
证明![]() ,然后根据全等三角形的性质得出
,然后根据全等三角形的性质得出![]() 、
、![]() 的长即可得出点
的长即可得出点![]() 的坐标;
的坐标;
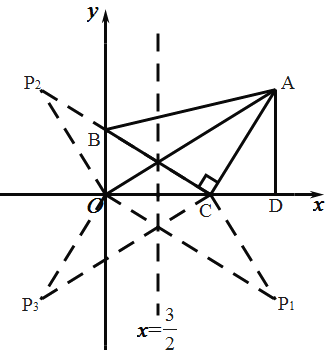
(2)做![]() 关于
关于![]() 轴的对称图形得到
轴的对称图形得到![]() ;做
;做![]() 关于
关于![]() 轴的对称图形得到
轴的对称图形得到![]() ;做
;做![]() 关于
关于![]() 轴的对称图形得到
轴的对称图形得到![]() ,根据对称图形的性质即可知道所作的图形全等,即可写出点
,根据对称图形的性质即可知道所作的图形全等,即可写出点![]() 的坐标;
的坐标;
(3)当以点![]() 为顶点时有一个点符合,当以点
为顶点时有一个点符合,当以点![]() 为顶点时分钝角三角形和锐角三角形即可求解.
为顶点时分钝角三角形和锐角三角形即可求解.
(1)∵点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]()
∴![]()
∵![]()
∴![]()
∵![]() 轴
轴
∴![]()
∴![]()
∴![]()
又∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴ 点![]() 的坐标为
的坐标为![]()
(2)①做![]() 关于
关于![]() 轴的对称图形得到
轴的对称图形得到![]() ,
,
∴![]()
∴点![]() 的坐标为
的坐标为![]() ;
;
②∵点![]() 和点
和点![]() 关于
关于![]() 对称
对称
∴做![]() 关于
关于![]() 轴的对称图形得到
轴的对称图形得到![]()
∴![]()
∴点![]() 的坐标为
的坐标为![]() ;
;
③做![]() 关于
关于![]() 轴的对称图形得到
轴的对称图形得到![]() ,
,
∴![]()
∴![]()
∴点![]() 的坐标为
的坐标为![]()
∴综上所述点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() ;
;
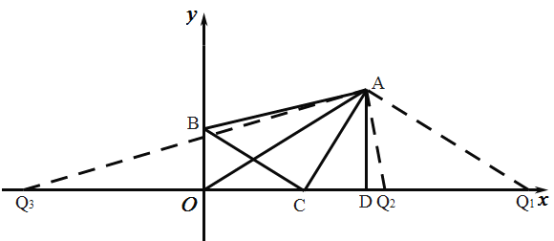
(3)①当以点![]() 为顶点时,且
为顶点时,且![]() 是腰
是腰
∵![]() 轴
轴
∴可以做点![]() 关于
关于![]() 的对称点
的对称点![]()
∴点![]() 的坐标为
的坐标为![]()
∴![]() 是
是![]() 的垂直平分线
的垂直平分线
∴![]()
∴![]() 是以
是以![]() 为腰的等腰三角形;
为腰的等腰三角形;
②当以点![]() 为顶点时,且
为顶点时,且![]() 是腰,形成锐角三角形时,
是腰,形成锐角三角形时,
即![]()
∴点![]() 的坐标为
的坐标为![]() ;
;
②当以点![]() 为顶点时,且
为顶点时,且![]() 是腰,形成钝角三角形时,
是腰,形成钝角三角形时,
即![]()
∴点![]() 的坐标为
的坐标为![]()
∴综上所述点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]()

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案【题目】某批彩色弹力球的质量检验结果如下表:
抽取的彩色弹力球数n | 500 | 1000 | 1500 | 2000 | 2500 |
优等品频数m | 471 | 946 | 1426 | 1898 | 2370 |
优等品频率 | 0.942 | 0.946 | 0.951 | 0.949 | 0.948 |
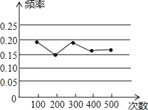
(1)请在图中完成这批彩色弹力球“优等品”频率的折线统计图

(2)这批彩色弹力球“优等品”概率的估计值大约是多少?(精确到0.01)
(3)从这批彩色弹力球中选择5个黄球、13个黑球、22个红球,它们除了颜色外都相同,将它们放入一个不透明的袋子中,求从袋子中摸出一个球是黄球的概率.
(4)现从第(3)问所说的袋子中取出若干个黑球,并放入相同数量的黄球,搅拌均匀,使从袋子中摸出一个黄球的概率为![]() ,求取出了多少个黑球?
,求取出了多少个黑球?