Question

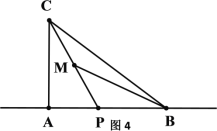
【题目】如图，在△ABC中，AB＝AC，AD是中线，且AC是DE的中垂线．

（1）求证：∠BAD＝∠CAD；

（2）连接CE，写出BD和CE的数量关系．并说明理由；

（3）当∠BAC＝90°，BC＝8时，在AD上找一点P，使得点P到点C与到点E的距离之和最小，并求出此时△BCP的面积．

Answer 1

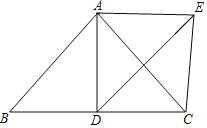
【答案】（1）详见解析；（2）BD＝CE，理由详见解析；（3）8

【解析】

（1）根据等腰三角形的性质即可得到结论；

（2）根据AC垂直平分DE，可得CD＝CE，又BD=CD即可证明；

（3）连接BE交AD于点P，此时PE+PC的值最小．先求出AD的长，再证明△APE≌△DPB，得出PA=PD，求出PD即可得出△BCP的面积．

（1）证明：∵AB＝AC，AD是中线，

∴∠BAD＝∠CAD；

（2）解：BD＝CE．理由如下：

∵AD是中线，∴BD＝CD，

∵AC垂直平分DE，∴CD＝CE，

∴BD＝CE；

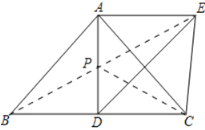
（3）解：连接BE，BE与AD的交点即为点P，

∵AB=AC，D为BC的中点，∴AD⊥BC，即AD垂直平分BC，

∴BP=CP，

∴PE+PC=PE+BP=BE，所以此时PE+PC的值最小．

∵AB＝AC，∠BAC＝90°，D为BC的中点，

∴AD⊥BC，∴∠ABC=∠ACB=45°=∠DAC=∠BAD，

∴AD＝BD=CD＝4，

由AC垂直平分DE得，AE＝AD=BD，

∴∠ADE=90°-∠DAC=45°=∠AED，

∴∠DAE=90°，

∴∠PAE=∠BDP=90°，

又∠BPD=∠EPA，

∴△APE≌△DPB（AAS），

∴PA＝PD＝2，

∵PD⊥BC，

∴S△BCP＝×8×2＝8．