题目内容
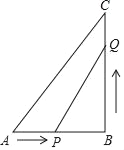
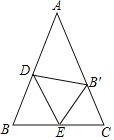
【题目】如图，在等腰△ABC中，AB＝AC，点D和点E分别在AB和BC上，连接DE，将△BDE沿DE翻折，点B的对应点B′刚好落在AC上，若AB'＝2B'C，AB＝3
，BC＝6，则BE的长为（ ）
A.3B.
C.
D.
【答案】D
【解析】
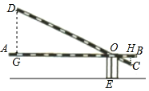
如图，过点A作AF⊥BC，B'H⊥BC，则B'H∥AF，由等腰三角形的可求BF＝CF＝3，由勾股定理可求AF＝6，由平行线分线段成比例可求B'H＝2，CH＝1，由勾股定理可求BE的长．
解：如图，过点A作AF⊥BC，B'H⊥BC，则B'H∥AF，
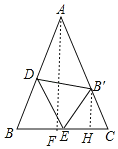
∵AB＝AC，AF⊥BC，
∴BF＝CF＝3，
∴AF＝
，
∵AB'＝2B'C，
∴AC＝3B'C，
∵AF∥B'H，
∴
，
∴CH＝1，B'H＝2，
∴BH＝5，
∵将△BDE沿DE翻折，
∴BE＝B'E，
∵B'E2＝B'H2+EH2，
∴BE2＝4+（5﹣BE）2，
∴BE＝
；
故选：D．
【题目】10月下旬，我校初三年级组织了体育期中测试．为了更好的了解孩子们的体育水平，全力备战中考，我校体育组从全年级体考成绩中随机抽查了20名男生和20名女生的体考成绩进行整理、描述和分析（成绩得分用x表示，共分成四组：A：47＜x≤50，B：44＜x≤47，C：41＜x≤44，D：x≤41），下面给出了部分信息：20名男生的体考成绩（单位：分）：50，46，50，50，47，49，39，46，49，46，46，43，49，47，40，48，44，42，45，44；20名女生的体考成绩为B等级的数据是：45，46，46，47，47，46，46．所抽取的学生体考成绩统计表
性别 | 平均数 | 中位数 | 众数 |
男 | 46 | 46 | b |
女 | 46.5 | c | 48 |
根据以上信息，解答下列问题：
（1）直接写出上述图表中a、b、c的值；
（2）根据以上数据，你认为我校男生的体育成绩好还是女生的体育成绩好？请说明理由（一条即可）；
（3）我校初三年级共有2400名学生参与此次体考测试，估计参加测试的学生等级为A的有多少人？
