Question

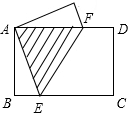
如图，一张边长为4的等边三角形纸片ABC，点E是边AB上的一个动点（不与A、B重合），EF∥BC交AC于点F．以EF为折痕对折纸片，当△AEF与四边形EBCF重叠部分的面积为

3

时，折痕EF的长度是（　　）

A．2

B． 2 3 或 8+ 10 3

C． 2 3

D．2或 10 3

Answer 1

在等边△ABC中，作AD⊥BC于D，交EF于H，
∴BD=DC=

1

2

BC=2．
又∵tan∠ABD=tan60°=

AD

BD

，
∴AD=2

3

；
∵EF∥BC，
∴△AEF∽△ABC．
∴

AH

AD

=

EF

BC

，

AH

2 3

=

EF

4

．
∴AH=

3

2

EF，
∴S_△AEF=

1

2

AH•EF．
S_△AEF=

1

2

•

3

2

EF²=

3

4

EF²．

①当折叠后△AEF的顶点A落在四边形BCFE内或BC边上时，
S_△AEF=

3

4

EF²=

3

，
解得，EF=2；

②当折叠后△AEF的顶点A落在四边形BCFE外点A′处时，如图所示，A′F交BC于M，A′E交BC于N，连接AA′交EF于H，交BC于D．
∵

AH

AD

=

EF

4

，
∴

AH

HD

=

EF

4-EF

，
又∵AH=A′H，
∴

A′H

HD

=

EF

4-EF

，
∴

A′H

A′D

=

EF

2EF-4

，
∴

S△A′EF

S△A′MN

=(

EF

2EF-4

)2，

3 4 EF2

S△A′MN

=

EF2

(2EF-4)2

，
∴S△A′MN=

3

4

(2EF-4)2．
∴S_{四边形MFEN}=

3

4

EF²-

3

4

(2EF-4)2=

3

，
解得，EF=

10

3

；
综上所述，EF的值是2或

10

3

．
故选D．