题目内容

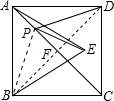
如图，正方形ABCD的对角线AC=6
2
，△ABE是等边三角形，点E在正方形ABCD内，若点P是对角线AC上的一个动点，则PE+PD的最小值为______．
连接BD，与AC交于点F．
∵点B与D关于AC对称，
∴PD=PB，
∴PD+PE=PB+PE=BE最小，
∵正方形ABCD的对角线为6
2
，
∴AB=6．
又∵△ABE是等边三角形，
∴BE=AB=6．
故所求最小值为6．
故答案为：6．
练习册系列答案
相关题目
把长方形ABCD沿AE折叠后，D点恰与BC边上的F重合，如图，已知AB=8，BC=10，求EC的长．
如图，将矩形ABCD沿对角线BD折叠，C点与E点重合，若AB=3，BC=9，求折叠后重叠部分（△BDF）的面积．
如图，方格纸中每个小方格都是边长为1的正方形，我们把以格点连线为边的多边形称为“格点多边形”．如图（一）中四边形ABCD就是一个“格点四边形”．
（1）作出四边形ABCD关于直线BD对称的四边形A′B′C′D′；
（2）求图（一）中四边形ABCD的面积；
（3）在图（二）方格纸中画一个格点三角形EFG，使△EFG的面积等于四边形ABCD的面积且△EFG为轴对称图形．
如图．在直角坐标系中，矩形ABC0的边OA在x轴上，边0C在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E．那么点D的坐标为（　　）
A．(-
4
5
，
12
5
)		B．(-
2
5
，
13
5
)		C．(-
1
2
，
13
5
)		D．(-
3
5
，
12
5
)
如图，一张边长为4的等边三角形纸片ABC，点E是边AB上的一个动点（不与A、B重合），EF∥BC交AC于点F．以EF为折痕对折纸片，当△AEF与四边形EBCF重叠部分的面积为
3
时，折痕EF的长度是（　　）
A．2B．
2
3
或
8+
10
3
C．
2
3
D．2或
10
3
已知矩形ABCD，现将矩形沿对角线BD折叠，得到如图所示的图形，
（1）求证：△ABE≌△C′DE；
（2）若AB=6，AD=10，求S△ABE．
如图，已知△ABC的三个顶点A、B、C的坐标分别是A（3，4），B（-2，1），C（1，-2）．
（1）请在平面直角坐标系xoy中，画出△ABC；
（2）以y轴为对称轴，将△ABC作轴对称变换，作出变换后所得的图象，并求出各个顶点的坐标．
如图a是长方形纸带，∠DEF=20°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是______度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网