题目内容
【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( ).

A. 4 B. ![]() C.
C. ![]() D. 2
D. 2
【答案】D
【解析】首先证明点P在以AB为直径的⊙O上,连接OC与⊙O交于点P,此时PC最小,利用勾股定理求出OC即可解决问题.
解:∵∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC,
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,
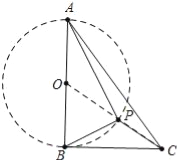
在RT△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC=![]() =5,
=5,
∴PC=OC=OP=5﹣3=2.
∴PC最小值为2.
故选B.
“点睛”本题考查了点与圆位置关系、圆周角定理、最短问题等知识,解题关键是确定点P位置,学会求圆外一点到圆的最小、最大距离,属于中考常考题型.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目





