题目内容
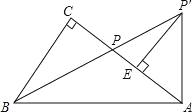
【题目】如图,在 Rt△ABC 中,∠C=90°,AP′⊥AB,BP′交 AC 于点 P, AP=AP′.
(1)求证:∠CBP=∠ABP;
(2)过点 P′作 P′E⊥AC 于点 E,求证:AE=CP.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据等腰三角形底角相等和∠CBP+∠BPC=90°,∠ABP+∠AP′
P=90°即可解题.
(2)过点 P 作 PD⊥AB 于 D,可证△APD≌△P′AE,可得 AE=CP.
解:(1)∵AP=AP′,
∴∠APP′=∠AP′P,
∵∠C=90°,AP′⊥AB,
∴∠CBP+∠BPC=90°,∠ABP+∠AP′P=90°,
又∵∠BPC=∠APP′(对顶角相等),
∴∠CBP=∠A BP;
(2)如图,过点 P 作 PD⊥AB 于 D,
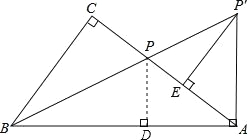
∵∠CBP=∠ABP,∠C=90°,
∴CP=DP,
∵P′E⊥AC,
∴∠EAP′+∠AP′E=90°, 又∵∠PAD+∠EAP′=90°,
∴∠PAD=∠AP′E,
在△APD 和△P′AE 中,
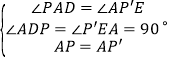 ,
,
∴△APD≌△P′AE(AAS),
∴AE=DP,
∴AE=CP.

练习册系列答案
相关题目