题目内容
【题目】如图,⊙O的半径为 ![]() ,BD是⊙O的切线,D为切点,过圆上一点C作BD的垂线,垂足为B,BC=3,点A是优弧CD的中点,则sin∠A的值是( )
,BD是⊙O的切线,D为切点,过圆上一点C作BD的垂线,垂足为B,BC=3,点A是优弧CD的中点,则sin∠A的值是( ) 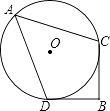
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解: 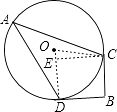
连接OC、OD,过C作CE⊥OD于E,
∵BD切⊙O于D,
∴BD⊥OD,
∵BC⊥BD,
∴∠B=∠BDE=∠CED=90°,
∴四边形CEDB是矩形,
∴BC=DE=3,
∵OD= ![]() ,
,
∴OE=OD﹣DE= ![]() ﹣3=
﹣3= ![]() ,
,
∴cos∠COE= ![]() =
= ![]() =
= ![]() ,
,
∵∠COD为弧CD对的圆心角,∠A为弧CD对的圆周角,
∴∠COD=2∠A,
∴cos2A= ![]() ,
,
∵1﹣2sin2A= ![]() ,
,
∴sinA= ![]() ,
,
故选C.
【考点精析】利用切线的性质定理对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
相关题目
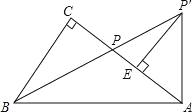
【题目】如图,在 Rt△ABC 中,∠C=90°,AP′⊥AB,BP′交 AC 于点 P, AP=AP′.
(1)求证:∠CBP=∠ABP;
(2)过点 P′作 P′E⊥AC 于点 E,求证:AE=CP.
【题目】七(1)班小明同学通过《测量硬币的厚度与质量》实验得到了每枚硬币的厚度和质量,数据如下表.他从储蓄罐取出一把5角和1元硬币,为了知道总的金额,他把这些硬币叠起来,用尺量出它们的总厚度为22.6mm,又用天平称出总质量为78.5g,请你帮助小明同学算出这把硬币的总金额为______元.
1元硬币 | 5角硬币 | |
每枚厚度(单位:mm) | 1.8 | 1.7 |
每枚质量(单位:g) | 6.1 | 6.0 |