��Ŀ����
����Ŀ����������֤�����̣�
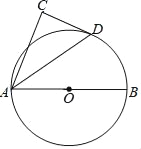
��ͼ��AB��CD��AD��BC��BEƽ�֡�ABC��DFƽ�֡�ADC��
��֤��BE��DF��

֤������AB��CD������֪��
���ABC+��C��180�㣮���� �� ��
�֡�AD��BC������֪��
���� ��+��C��180�㣮���� �� ��
���ABC����ADC������ �� ��
��BEƽ�֡�ABC������֪��
���1��![]() ��ABC������ �� ��
��ABC������ �� ��
ͬ������2��![]() ��ADC��
��ADC��
���� ������2��
��AD��BC������֪��
���2����3������ �� ��
���1����3��
��BE��DF������ �� ��
���𰸡���ֱ��ƽ�У�ͬ���ڽǻ�������ADC����ֱ��ƽ�У�ͬ���ڽǻ�����ͬ�ǵIJ�����ȣ��ǵ�ƽ���ߵĶ��壻��1����ֱ��ƽ�У��ڴ�����ȣ�ͬλ����ȣ���ֱ��ƽ�У�
��������
����ƽ���ߵ�����֪��ABC+��C=��ADC+��C=180��֪��ABC=��ADC�����ݽ�ƽ���ߵĶ���֤��1=��2�����AD��BC�á�2=��3������ƽ���ߵ����ʵá�1=��3���Ӷ���֤��
֤������AB��CD������֪��
���ABC+��C=180�㣮����ֱ��ƽ�У�ͬ���ڽǻ�����
�֡�AD��BC������֪��
���ADC+��C=180�㣮����ֱ��ƽ�У�ͬ���ڽǻ�����
���ABC=��ADC����ͬ�ǵIJ�����ȣ�
��BEƽ�֡�ABC������֪��
���1=![]() ��ABC�����ǵ�ƽ���ߵĶ��壩
��ABC�����ǵ�ƽ���ߵĶ��壩
ͬ������2=![]() ��ADC��
��ADC��
���1=��2��
��AD��BC������֪��
���2=��3������ֱ��ƽ�У��ڴ�����ȣ�
���1=��3��
��BE��DF����ͬλ����ȣ���ֱ��ƽ�У�
�ʴ�Ϊ����ֱ��ƽ�У�ͬ���ڽǻ�������ADC����ֱ��ƽ�У�ͬ���ڽǻ�����ͬ�ǵIJ�����ȣ��ǵ�ƽ���ߵĶ��壻��1����ֱ��ƽ�У��ڴ�����ȣ�ͬλ����ȣ���ֱ��ƽ�У�

 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�