题目内容
【题目】函数y=mx2﹣2mx﹣3m是二次函数.
(1)如果该二次函数的图象与y轴的交点为(0,3),求m的值;
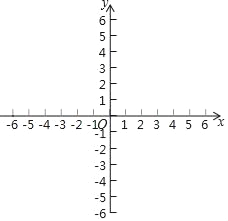
(2)在给定的坐标系中画出(1)中二次函数的图象.
【答案】(1)m=﹣1;(2)画图见解析.
【解析】
(1)由抛物线与y轴交于(0,3),将x=0,y=3代入抛物线解析式,即可求出m的值;(2)由(1)求得解析式,配方后找出顶点坐标,根据确定出的解析式列出相应的表格,由表格得出7个点的坐标,在平面直角坐标系中描出7个点,然后用平滑的曲线作出抛物线的图象.
(1)∵该函数的图象与y轴交于点(0,3),
∴把x=0,y=3代入解析式得:﹣3m=3,
解得m=﹣1;
(2)由(1)可知函数的解析式为y=﹣x2+2x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴顶点坐标为(1,4);
列表如下:
x | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 |
y | ﹣5 | 0 | 3 | 4 | 3 | 0 | ﹣5 |
描点;
画图如下:

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目