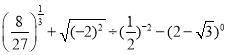题目内容
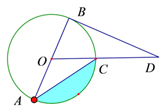
【题目】如图，BD是⊙O的切线，B为切点，连接DO与⊙O交于点C，AB为⊙O的直径，连接CA，若∠D=30°，⊙O的半径为4.
(1) 求∠BAC的大小；
(2) 求图中阴影部分的面积．
【答案】(1)30°;(2) 
【解析】试题分析：（1）先由切线的性质得出∠DBA＝90°，根据直角三角形的两锐角互余求出∠BOC＝60°，然后根据同弧所对的圆周角是圆心角的一半即可得出答案；
（2）由条件可求得∠COA的度数，过O作OE⊥CA于点E，则可求得OE的长和CA的长，再利用S阴影＝S扇形COA－S△COA可求得答案．
试题解析：
解：（1）∵DB为⊙O的切线，
∴
，
∵
∴
；
（2）如图，过O作OE⊥CA于点E，
∵
∴
∵
∴OE＝2，
∴
，
，
∴
阴影＝
扇形COA﹣
△COA＝
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
