题目内容
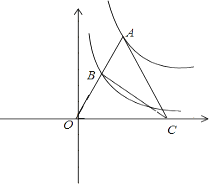
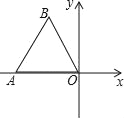
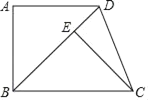
【题目】如图1,小明将一张长为4、宽为3的矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用点F表示).
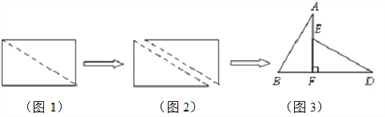
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的△ABF沿BD向右平移到图4中![]() 的位置,其中点B与点F 重合,请你求出平移的距离 ;
的位置,其中点B与点F 重合,请你求出平移的距离 ;
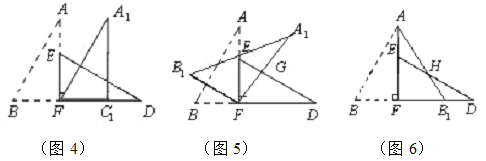
(2)在图5中若∠GFD=60°,则图3中的△ABF绕点 按 方向旋转 到图5的位置;
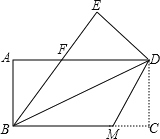
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,试问:△AEH和△HB1D的面积大小关系.说明理由.
【答案】(1)3;(2)点F、顺时针、30°(或者逆时针、330°)(3)相等,理由见解析.
【解析】(1)根据题意,分析可得:图形平移的距离就是线段BC1的长,进而在Rt△ABC中求得BC1=3cm,即图形平移的距离是3cm;
(2))先根据∠GFD=60°,得出∠AFA1=30°,即可得出图3中的△ABF绕点按F顺时针方向旋转30°到图5的位置;
(3)借助平移的性质,经过平移,对应点所连的线段平行且相等,对应线段平行且相等,即可证出△AHE≌△DHB1,从而得出△AEH和△HB1D的面积相等.
试题解析:(1)图形平移的距离就是线段BC1的长,
又∵在Rt△ABC中,长为4、宽为3,
∴BF=3cm,
∴平移的距离为3cm,
故答案为:3;
(2)∵∠GFD=60°,
∴∠AFA1=30°,
图3中的△ABF绕点按F顺时针方向旋转30°到图5的位置,
故答案为:F,顺时针,30°;
(3)相等,理由如下:
在△AHE与△DHB1中,
∵∠FAB1=∠EDF=30°,
∵FD=FA,EF=FB=FB1,
∴FD-FB1=FA-FE,即AE=DB1,
又∵∠AHE=∠DHB1,
∴△AHE≌△DHB1(AAS),
∴![]() .
.

 小题狂做系列答案
小题狂做系列答案