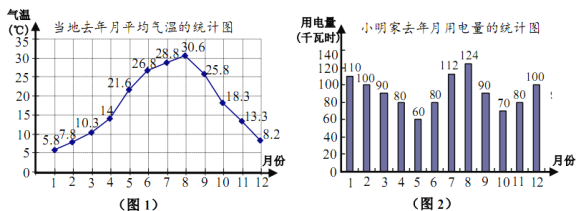
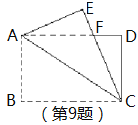
��Ŀ����
����Ŀ����ͼ��ij�յ�Ǯ�����۳���Ϣ�����

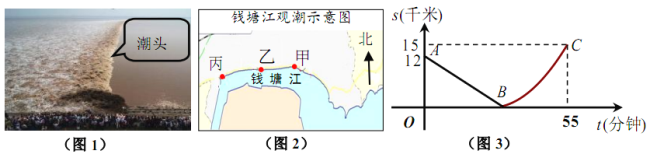
��������Ϣ��С�콫�����泱���γɺ�ͷ���ҵ�֮��ľ���![]() ��ǧ�ף���ʱ��
��ǧ�ף���ʱ��![]() �����ӣ��ĺ�����ϵ��ͼ3��ʾ�����У���11:40ʱ�������泱���ij�ͷ���ҵ�12ǧ������Ϊ��
�����ӣ��ĺ�����ϵ��ͼ3��ʾ�����У���11:40ʱ�������泱���ij�ͷ���ҵ�12ǧ������Ϊ��![]() ����
����![]() ����Ϊ
����Ϊ![]() ������
������![]() ���ö��κ���
���ö��κ���![]() ��
��![]() ��
��![]() �dz������̻���
�dz������̻���
��1����![]() ��ֵ���������ͷ�Ӽص��ҵص��ٶȣ�
��ֵ���������ͷ�Ӽص��ҵص��ٶȣ�
��2��11:59ʱ��С���ﵥ�����ҵس������ؽ��߹�·��![]() ǧ��/�ֵ��ٶ����ط���ȥ���������������Ӻ��볱ͷ������
ǧ��/�ֵ��ٶ����ط���ȥ���������������Ӻ��볱ͷ������
��3��������С��������ת��ͷ���ؽ��߹�·����ͷ�ٶ��볱ͷ���У�����ͷ���ҵغ���ȼ��٣�����������ٶ�Ϊ![]() ǧ��/�֣�С���������С���볱ͷ���������ͷ1.8ǧ����ʱ�䣿����ˮ���ٽ��ٶ�
ǧ��/�֣�С���������С���볱ͷ���������ͷ1.8ǧ����ʱ�䣿����ˮ���ٽ��ٶ�![]() ��
��![]() �Ǽ���ǰ���ٶȣ���
�Ǽ���ǰ���ٶȣ���
���𰸡���1��m=30��0.4ǧ��/���ӣ���2��5��������3��С���볱ͷ��������ͷ����1.8ǧ�����Ҫ26����.
��������
�����������1���������֪������30���Ӻ��ҵأ��Ӷ���֪m=30�����ڼص��ҵ��������˶�����������·�̳���ʱ�伴������ٶȣ�
��2�����ڳ�ͷ���ٶ�Ϊ0.4ǧ��/���ӣ����Ե�11��59ʱ����ͷ��ǰ��19��0.4=7.6ǧ�ף���С�����x���ӣ����������г����̼������x��ֵ��
��3�������s�Ľ���ʽ�����ݳ�ˮ���ٽεĹ�ϵʽ�������ͷ���ٶȴﵽ��������ٶ�0.48ǧ��/����ʱ����Ӧ��ʱ��t���Ӷ���֪��ͷ���ҵ�֮��ľ���s���������ҵصľ���Ϊs1����s1��ʱ��t�ĺ�����ϵʽΪs1=0.48t+h��t��35������t=35ʱ��s1=s= ![]() ���Ӷ������h��ֵ�����ͷ��С�����1.8ǧ��ʱ����s-s1=1.8���Ӷ������t��ֵ������С���볱ͷ��������ͷ�ٶ��볱ͷ���е����ҵ���ʱ6���ӣ�����Ҫʱ��Ϊ6+50-30=26���ӣ�
���Ӷ������h��ֵ�����ͷ��С�����1.8ǧ��ʱ����s-s1=1.8���Ӷ������t��ֵ������С���볱ͷ��������ͷ�ٶ��볱ͷ���е����ҵ���ʱ6���ӣ�����Ҫʱ��Ϊ6+50-30=26���ӣ�
�����������1���������֪��m=30��
��B��30��0����
��ͷ�Ӽص��ҵص��ٶ�Ϊ��![]() ��0.4ǧ��/���ӣ�
��0.4ǧ��/���ӣ�
��2���߳�ͷ���ٶ�Ϊ0.4ǧ��/���ӣ�
�ൽ11��59ʱ����ͷ��ǰ��19��0.4=7.6ǧ�ף�
��С�����x�����볱ͷ������
��0.4x+0.48x=12-7.6��
��x=5
��С��5�����볱ͷ������
��3���ѣ�30��0����C��55��15������s=![]() t2+bt+c��
t2+bt+c��
��ã�b=-![]() ��c=-
��c=-![]() ��
��
��s=![]() t2-
t2-![]() t-
t-![]()
��v0=0.4��
��v=![]() ��t-30��+
��t-30��+![]() ��
��
����ͷ���ٶȴﵽ��������ٶ�0.48ǧ��/���ӣ�
��ʱv=0.48��
��0.48=![]() ��t-30��+
��t-30��+![]() ��
��
��t=35��
��t=35ʱ��
s=![]() t2-
t2-![]() t-
t-![]() =
=![]() ��
��
���t=35�֣�12��15ʱ����ʼ����ͷ����С���ٶȱ�����أ�С�������С������0.48ǧ��/�ֵ��ٶ������ϳ�ͷ��
�������ҵصľ���Ϊs1����s1��ʱ��t�ĺ�����ϵʽΪs1=0.48t+h��t��35����
��t=35ʱ��s1=s=![]() ������ɵã�h=-
������ɵã�h=-![]() ��
��
��s1=![]() t-
t-![]()
���ͷ��С�����1.8ǧ��ʱ����s-s1=1.8��
��![]() t2-
t2-![]() t-
t-![]() -
-![]() t+
t+![]() =1.8
=1.8
��ã�t=50��t=20�����������⣬��ȥ����
��t=50��
С���볱ͷ��������ͷ�ٶ��볱ͷ���е����ҵ���ʱ6���ӣ�
���Ҫʱ��Ϊ6+50-30=26���ӣ�
��С���볱ͷ��������ͷ����1.8ǧ�����Ҫ26����.