题目内容
【题目】有甲乙两个玩具小汽车在笔直的240米跑道![]() 上进行折返跑游戏,甲从点
上进行折返跑游戏,甲从点![]() 出发,匀速在
出发,匀速在![]() 、
、![]() 之间折返跑,同时乙从点
之间折返跑,同时乙从点![]() 出发,以大于甲的速度匀速在
出发,以大于甲的速度匀速在![]() 、
、![]() 之间折返跑.在折返点的时间忽略不计.
之间折返跑.在折返点的时间忽略不计.

(1)若甲的速度为![]() ,乙的速度为
,乙的速度为![]() ,第一次迎面相遇的时间为
,第一次迎面相遇的时间为![]() ,则
,则![]() 与
与![]() 的关系式___________;
的关系式___________;
(注释:当两车相向而行时相遇是迎面相遇,当两车在![]() 点相遇时也视为迎面相遇)
点相遇时也视为迎面相遇)
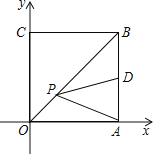
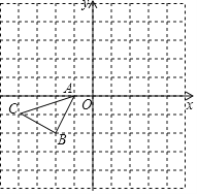
(2)如图1,
①若甲乙两车在距![]() 点20米处第一次迎面相遇,则他们在距
点20米处第一次迎面相遇,则他们在距![]() 点_______米第二次迎面相遇:
点_______米第二次迎面相遇:
②若甲乙两车在距![]() 点50米处第一次迎面相遇,则他们在距
点50米处第一次迎面相遇,则他们在距![]() 点__________米第二次迎面相遇;
点__________米第二次迎面相遇;
(3)设甲乙两车在距![]() 点
点![]() 米处第一次迎面相遇,在距
米处第一次迎面相遇,在距![]() 点
点![]() 米处第二次迎面相遇.某同学发现了
米处第二次迎面相遇.某同学发现了![]() 与
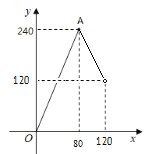
与![]() 的函数关系,并画出了部分函数图象(线段
的函数关系,并画出了部分函数图象(线段![]() ,不包括点
,不包括点![]() ,如图2所示).
,如图2所示).
①则![]() _______,并在图2中补全
_______,并在图2中补全![]() 与
与![]() 的函数图象(在图中注明关键点的数据);
的函数图象(在图中注明关键点的数据);
②分别求出各部分图象对应的函数表达式.
【答案】(1)![]() ;(2)①60②150 ;(3)①80,②当0<x≤80时,y=3x;当80≤x<120时,
;(2)①60②150 ;(3)①80,②当0<x≤80时,y=3x;当80≤x<120时,![]()
【解析】
(1)根据相遇问题知识列出代数式整理即可;
(2)①当他们第一次相遇时,他们一共行驶了1个全程,当他们第二次迎面相遇时,他们共行驶了3个全程,从而找到甲走的路程即可;②和前面①一样的方法算出即可;
(3)①当他们第二次迎面相遇时,他们共行驶了3个全程,则240÷3=80,求出a的值,当x>80时,则当他们第二次迎面相遇时,距M点的距离为240-(3x-240)=480-3x米,从而补全函数图像;②根据图像上点的坐标分别求出解析式即可.
(1) 甲的速度为![]() ,乙的速度为
,乙的速度为![]() ,第一次迎面相遇的时间为
,第一次迎面相遇的时间为![]() ,
,
则![]() ,
,
∴![]() ;
;
(2)①当他们第一次相遇时,他们一共行驶了1个全程,当他们第二次迎面相遇时,他们共行驶了3个全程,
若甲乙两车在距![]() 点20米处第一次迎面相遇,
点20米处第一次迎面相遇,
则他们一共行驶一个全程时,甲走了20米,
当他们第二次迎面相遇时,他们共行驶了3个全程,
∴甲走了20×3=60米,
则他们在距![]() 点60米第二次迎面相遇;
点60米第二次迎面相遇;
②若甲乙两车在距![]() 点50米处第一次迎面相遇,
点50米处第一次迎面相遇,
则他们一共行驶一个全程时,甲走了50米,
当他们第二次迎面相遇时,他们共行驶了3个全程,
∴甲走了50×3=150米,
则他们在距![]() 点150米第二次迎面相遇;
点150米第二次迎面相遇;
(3)①当他们第二次迎面相遇时,他们共行驶了3个全程,
则240÷3=80,
则a的值为80,
∵乙的速度大于甲的速度,
∴他们一共行驶一个全程时,甲走的路程<120米,
当x>80时,
则当他们第二次迎面相遇时,距M点的距离为240-(3x-240)=480-3x米,
补全函数图像,如图所示:
②当0<x≤80时,
设函数解析式为y=kx+b,把(0,0),(80,240)代入得
![]() ,
,
解得;![]() ,
,
∴y=3x;
当80≤x<120时,把(80,120),(120,120)代入得:
![]()
解得;![]() ,
,
∴![]() .
.

【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为176mm~185mm的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据:(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183
整理数据:
频数 组别 | 165.5~170.5 | 170.5~175.5 | 175.5~180.5 | 180.5~185.5 | 185.5~190.5 | 190.5~195.5 |
甲车间 | 2 | 4 | 5 | 6 | 2 | 1 |
乙车间 | 1 | 2 | a | 6 | 2 | 0 |
分析数据:
车间 | 平均数 | 众数 | 中位数 | 方差 |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
应用数据:
(1)计算甲车间样品的合格率;
(2)估计乙车间生产的8000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.