题目内容
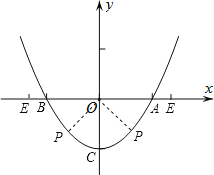
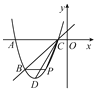
【题目】已知抛物线y＝x2﹣2和x轴交于A，B（点A在点B右边）两点，和y轴交于点C，P为抛物线上的动点．
（1）求出A，C的坐标；
（2）求动点P到原点O的距离的最小值，并求此时点P的坐标；
（3）当点P在x轴下方的抛物线上运动时，过P的直线交x轴于E，若△POE和△POC全等，求此时点P的坐标．
【答案】（1）A（﹣
，0），点C的坐标为（0，﹣2）；（2）最小值为
，点P的坐标为（
，﹣
）或（﹣，﹣）；（3）P（﹣1，﹣1）或（1，1）．
【解析】
（1）令y＝0，解方程求出x的值，即可得到点A、B的坐标，令x＝0求出y的值，即可得到点C的坐标；
（2）根据二次函数图象上点的坐标特征设点P的坐标为（x，x2﹣2），利用勾股定理列式求出OP2，再根据二次函数的最值问题解答；
（3）根据二次函数的增减性，点P在第三四象限时，OP≠1，从而判断出OC与OE是对应边，然后确定出点E与点A或点B重合，再根据全等三角形对应角相等可得∠POC＝∠POE，然后根据第三、四象限角平分线上的点到角的两边距离相等的坐标特征利用抛物线解析式求解即可．
解：（1）令y＝0，则x2﹣2＝0，
解得x＝±，
∵点A在点B右边，
∴A（
，0），
令x＝0，则y＝﹣2，
∴点C的坐标为（0，﹣2）；
（2）∵P为抛物线y＝x2﹣2上的动点，
∴设点P的坐标为（x，x2﹣2），
则OP2＝x2+（x2﹣2）2＝x4﹣3x2+4＝（x2﹣
）2+
，
∴当x2＝，即x＝±时，OP2最小，OP的值也最小，最小值为，
此时，点P的坐标为（，﹣）或（﹣，﹣）；
（3）∵OP2＝（x2﹣）2+，
∴点P在第三四象限时，OP≠1，
∵△POE和△POC全等，
∴OC与OE是对应边，
∴∠POC＝∠POE，
∴点P在第三、四象限角平分线上，
①点P在第三象限角平分线上时，y＝x，
∴x2﹣2＝x，
解得x1＝﹣1，x2＝2（舍去），
此时，点P（﹣1，﹣1）；
②点P在第四象限角平分线上时，y＝﹣x，
∴x2﹣2＝﹣x，
解得x1＝1，x2＝﹣2（舍去），
此时，点P（1，1），
综上所述，P（﹣1，﹣1）或（1，1）时△POE和△POC全等．
