题目内容
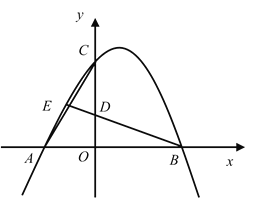
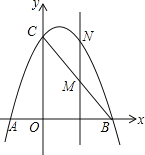
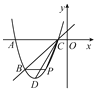
【题目】如图，已知抛物线y=ax2＋bx＋5经过A(－5，0)，B(－4，－3)两点，与x轴的另一个交点为C，顶点为D，连接CD．
（1）求该抛物线的解析式；
（2）点P为该抛物线上一动点(与点B，C不重合)，设点P的横坐标为t．当点P在直线BC的下方运动时，求△PBC的面积的最大值．
【答案】（1）
；（2）
【解析】
（1）将A、B两点坐标代入抛物线，求解即可得出其解析式；
（2）首先求出直线BC解析式，然后设点
，则点
，利用△PBC面积构建一元二次方程，即可求出最值.
（1）由题意，得将A(－5，0)，B(－4，－3)代入抛物线，得
解得
∴该抛物线的解析式为；
（2）令
，则
或-5，即点C（-1,0）
过点P作
轴的平行线交BC于点G，如图所示：
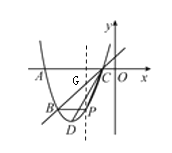
设直线BC的解析式为
将B、C的坐标代入一次函数表达式，得
解得
直线BC为
设点，则点
则
∴当
时，其最大值为.
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
【题目】某宾馆有若干间标准房，当标准房的价格为200元时，每天入住的房间数为60间，经市场调查表明，该宾馆每间标准房的价格在170~240元之间（含170元，240元）浮动时，每天入住的房间数
（间）与每间标准房的价格
（元）的数据如下表：
| … | 190 | 200 | 210 | 220 | … |
| … | 65 | 60 | 55 | 50 | … |
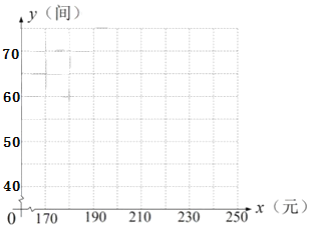
（1）根据所给数据在坐标系中描出相应的点，并画出图象.
（2）求关于的函数表达式、并写出自变量的取值范围.
（3）设客房的日营业额为
（元）.若不考虑其他因素，问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元？
