题目内容
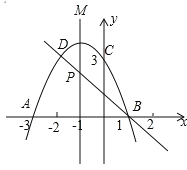
【题目】已知直线![]() 与双曲线
与双曲线![]()
![]() 交于
交于![]() ,
,![]() 两点,过
两点,过![]() 作
作![]() 轴于点
轴于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.

(Ⅰ)求![]() ,
,![]() 两点的坐标;
两点的坐标;
(Ⅱ)试探究直线![]() 与
与![]() 的位置关系并说明理由.
的位置关系并说明理由.
(Ⅲ)已知点![]() ,且
,且![]() ,
,![]() 在抛物线
在抛物线![]()
![]() 上,若当
上,若当![]() (其中
(其中![]() )时,函数
)时,函数![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)若![]() ,则
,则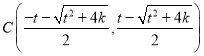 ,
,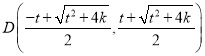 ,若
,若![]() ,则
,则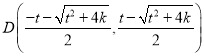 ,
,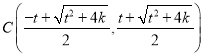 ;(Ⅱ)
;(Ⅱ)![]() ,理由见解析;(Ⅲ)
,理由见解析;(Ⅲ)![]() 的值为
的值为![]()
【解析】
(Ⅰ)把直线y=x+t与双曲线![]() 的解析式联立成方程组,解方程组即可求出交点坐标,即C、D两点的坐标;
的解析式联立成方程组,解方程组即可求出交点坐标,即C、D两点的坐标;
(Ⅱ)位置关系是:平行,求出直线AB的解析式,与直线CD的解析式y=x+t比较,k相等说明两直线平行;
(Ⅲ)先求出C点坐标,再利用待定系数法求出抛物线的解析式,最后通过分类讨论:①当![]() 时,②当
时,②当![]() ,③当
,③当![]() ,分别根据函数
,分别根据函数![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]() ,结合二次函数的性质列出方程,得出m,n的值.
,结合二次函数的性质列出方程,得出m,n的值.
解:(Ⅰ)联立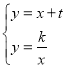 ,解得:
,解得: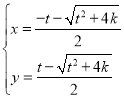 或
或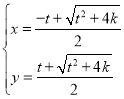 ,
,
设![]() ,
,![]() ,
,
若![]() ,则
,则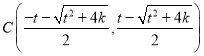 ,
,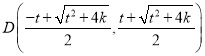 ,
,
若![]() ,则
,则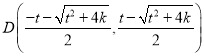 ,
,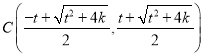 ;
;
(Ⅱ)![]() ,
,
理由:不妨设![]() ,
,
由(1)知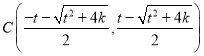 ,
, 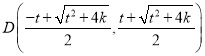 ,
,
∴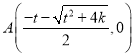 ,
,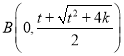 ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则将![]() ,
,![]() 两点坐标代入有:
两点坐标代入有:![]() ,
,![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
∴直线![]() 与
与![]() 的位置关系是
的位置关系是![]() ;
;
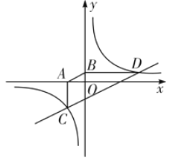
(Ⅲ)将![]() 代入双曲线
代入双曲线![]()
![]() 得
得![]() ,
,
将![]() 代入直线
代入直线![]() ,得
,得![]() ,
,
∵![]() ,
,
∴由(Ⅰ)知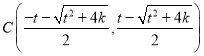 ,
,
∴![]() ,
,
∵![]() ,
,![]() 在抛物线
在抛物线![]()
![]() 上,
上,
∴![]() ,解得
,解得![]() ,
,
即![]() ,
,
由![]() ,可知
,可知![]() ,
,![]() ,
,
①当![]() 时,由函数的最小值为
时,由函数的最小值为![]() ,最大值为
,最大值为![]() ,可知
,可知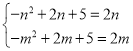 ,
,
∴![]() ,
,![]() 即为一元二次方程
即为一元二次方程![]() 的两解,即
的两解,即![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
又∵![]() ,
,
∴此情况不合题意;
②当![]() ,即
,即![]() 时,
时,
由函数的最小值为![]() ,最大值为
,最大值为![]() ,可知
,可知![]() ,
,
解得: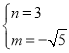 ,
,
此时![]() ,即
,即![]() ,符合题意,
,符合题意,
∴![]() ;
;
③当![]() ,即
,即![]() 时,
时,
由函数的最小值为![]() ,最大值为
,最大值为![]() ,可知
,可知![]() ,
,
解得:![]() ,
,
∵![]() ,
,
∴此情况不合题意,
综上所述,满足题意的![]() 的值为
的值为![]() .
.

【题目】某同学在利用描点法画二次函数y=ax2+bx+c(a=0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣3 | 0 | ﹣1 | 0 | 3 | … |
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()