题目内容
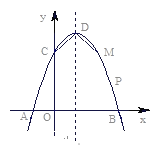
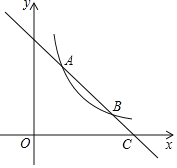
【题目】如图,一次函数y=﹣x+3的图象与反比例函数y=![]() (k≠0)在第一象限的图象交于A(1,a)和B两点,与x轴交于点C.
(k≠0)在第一象限的图象交于A(1,a)和B两点,与x轴交于点C.
(1)求反比例函数的解析式及点A的坐标;
(2)若点P为x轴上一点,且满足△ACP是等腰三角形,请直接写出符合条件的所有点P的坐标.
【答案】(1)y=![]() ,(1,2);(2) (﹣1,0)或(3﹣2
,(1,2);(2) (﹣1,0)或(3﹣2![]() ,0)或(3+2
,0)或(3+2![]() ,0)或(1,0)
,0)或(1,0)
【解析】
(1)利用点A在y=﹣x+3上求a,进而代入反比例函数y=![]() (k≠0)求k即可;
(k≠0)求k即可;
(2)根据已知条件得到C(3,0),根据两点间的距离公式得到AC=![]() ,过A作AD⊥x轴于D,当AP=AC时,当AC=CP=2
,过A作AD⊥x轴于D,当AP=AC时,当AC=CP=2![]() 时,当AP=CP时,根据等腰三角形的性质即可得到结论.
时,当AP=CP时,根据等腰三角形的性质即可得到结论.
解:(1)把点A(1,a)代入y=﹣x+3,得a=2,
∴A(1,2)
把A(1,2)代入反比例函数y=![]() ,
,
∴k=1×2=2;
∴反比例函数的表达式为y=![]() ;
;
(2)∵一次函数y=﹣x+3的图象与x轴交于点C,
∴C(3,0),
∵A(1,2),
∴AC=![]() ,
,
过A作AD⊥x轴于D,
∴OD=1,CD=AD=2,
当AP=AC时,PD=CD=2,
∴P(﹣1,0),
当AC=CP=2![]() 时,△ACP是等腰三角形,
时,△ACP是等腰三角形,
∴OP=3﹣2![]() 或OP=3+2
或OP=3+2![]()
∴P(3﹣2![]() ,0)或(3+2
,0)或(3+2![]() ,0),
,0),
当AP=CP时,△ACP是等腰三角形,此时点P与D重合,
∴P(1,0),
综上所述,所有点P的坐标为(﹣1,0)或(3﹣2![]() ,0)或(3+2
,0)或(3+2![]() ,0)或(1,0).
,0)或(1,0).

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案【题目】某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间,经市场调查表明,该宾馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数![]() (间)与每间标准房的价格
(间)与每间标准房的价格![]() (元)的数据如下表:
(元)的数据如下表:
| … | 190 | 200 | 210 | 220 | … |
| … | 65 | 60 | 55 | 50 | … |
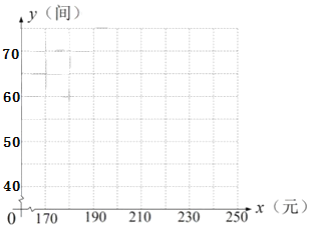
(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)求![]() 关于
关于![]() 的函数表达式、并写出自变量
的函数表达式、并写出自变量![]() 的取值范围.
的取值范围.
(3)设客房的日营业额为![]() (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
(元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
【题目】1995年联合国教科文组织把每年4月23日确定为“世界读书日”.某中学为了解全校1000名学生平均每天阅读课外书报的时间,随机调查了该校50名学生一周内平均每天阅读课外书报的时间,结果如下表:
时间(分) | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
人 数 | 8 | 12 | 7 | 5 | 4 | 3 | 4 | 2 | 3 | 2 |
根据上述信息完成下列各题:
(1)在统计表(上表)中,众数是 分,中位数是 分;
(2)估计该学校平均每天阅读课外书报的时间不少于35分钟的学生大约 人;
小明同学根据上述信息制作了如下频数分布表和频数分布直方图,请你完成下列问题:
(3)频数分布表中![]() ,
,![]() ;
;
(4)补全频数分布直方图.

【题目】如图,P是半圆O中![]() 所对弦AB上一动点,过点P作PM⊥AB交
所对弦AB上一动点,过点P作PM⊥AB交![]() 于点M,作射线PN交
于点M,作射线PN交![]() 于点N,使得∠NPB=45°,连接MN.已知AB=6cm,设A,P两点间的距离为xcm,M,N两点间的距离为ycm.(当点P与点A重合时,点M也与点A重合,当点P与点B重合时,y的值为0)
于点N,使得∠NPB=45°,连接MN.已知AB=6cm,设A,P两点间的距离为xcm,M,N两点间的距离为ycm.(当点P与点A重合时,点M也与点A重合,当点P与点B重合时,y的值为0)
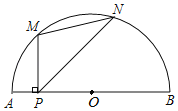
小超根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小超的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,得到了y与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 4.2 | 2.9 | 2.6 | 2.0 | 1.6 | 0 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当MN=2AP时,AP的长度约为 cm.