题目内容
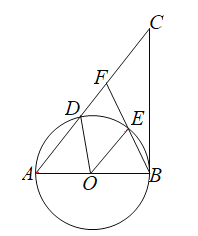
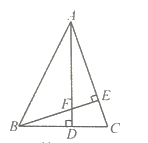
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,以
的中点,以![]() 为直角边向外作等腰
为直角边向外作等腰![]() ,连接
,连接![]() ,当
,当![]() 取最大值时,则
取最大值时,则![]() 的度数是________.
的度数是________.
【答案】22.5°
【解析】
由旋转的性质可得OB=BE,OD=CE,∠BCE=∠BDO,∠OBE=90°,由三角形三边关系可得CE≤OC+OE,即当点O在CE上时,CE有最大值,即OD取最大值,由直角三角形的性质可求解.
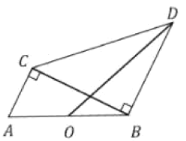
解:如图,将△ODB绕点B逆时针旋转90°,得到△ECB,连接CO,EO,
∵将△ODB绕点B逆时针旋转90°,得到△ECB,
∴OB=BE,OD=CE,∠BCE=∠BDO,∠OBE=90°
∵CE≤OC+OE
∴当点O在CE上时,CE有最大值,即OD取最大值,
∵BE=OB,∠ABE=90°
∴∠BOE=45°
∵点O是AB中点,∠ACB=90°
∴CO=BO
∴∠ECB=∠CBO,
∵∠EOB=∠ECB+∠OBC=45°
∴∠ECB=22.5°=∠BDO
故答案为:22.5°.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目