��Ŀ����
����Ŀ����֪�����κ���![]() ��
��![]() ͼ��Ķ���ֱ�ΪA��B������m��aΪʵ��������C������Ϊ��0��
ͼ��Ķ���ֱ�ΪA��B������m��aΪʵ��������C������Ϊ��0��![]() ����
����
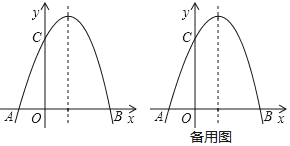
��1�����жϺ���![]() ��ͼ���Ƿ���C����˵�����ɣ�
��ͼ���Ƿ���C����˵�����ɣ�
��2����mΪ����ʵ��ʱ������![]() ��ͼ��ʼ�վ�����C����a��ֵ��
��ͼ��ʼ�վ�����C����a��ֵ��
��3���ڣ�2���������£����ڲ�Ψһ��xֵ����x����ʱ������![]() ��ֵ��С�Һ���
��ֵ��С�Һ���![]() ��ֵ����
��ֵ����
��ֱ��д��m�ķ�Χ��
�ڵ�PΪx��������ԭ��O������һ�㣬����P��y���ƽ���ߣ��뺯��![]() ��
��![]() ��ͼ��ֱ��ཻ�ڵ�D��E����˵��
��ͼ��ֱ��ཻ�ڵ�D��E����˵��![]() ��ֵֻ���P��λ���йأ�
��ֵֻ���P��λ���йأ�
���𰸡���1������y1��ͼ����C������������2��![]() ����3����
����3����![]() ���ڼ�����
���ڼ�����
��������
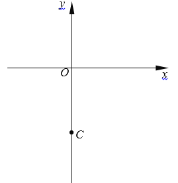
��1��ȡx=0ʱ�������![]() ��˵������
��˵������![]() ��ͼ����C��
��ͼ����C��
��2������C��0��![]() ������
������![]() ��
��![]() �����a��ֵ��
�����a��ֵ��
��3����ֻҪ![]() �ĶԳ���ʼ����
�ĶԳ���ʼ����![]() �ĶԳ����Ҳ࣬��������Ŀ��Ҫ�ó�m�ķ�Χ��
�ĶԳ����Ҳ࣬��������Ŀ��Ҫ�ó�m�ķ�Χ��
�����P��������![]() ��0�������DE=
��0�������DE=![]() �����ù��ɶ������AB=
�����ù��ɶ������AB=![]() ������˵������.
������˵������.
��1������![]() ��ͼ����C�� �������£�
��ͼ����C�� �������£�
��x=0ʱ��![]() =
=![]() =
=![]() ��
��
�ຯ��![]() ��ͼ����C��
��ͼ����C��
��2������C��0��![]() ������
������![]() �ã�
�ã�
![]() ����
����![]() ����mΪ����ʵ��ʱ������
����mΪ����ʵ��ʱ������![]() ��ͼ��ʼ�վ�����C��
��ͼ��ʼ�վ�����C��
��![]() �ij�����m�أ�
�ij�����m�أ�
��![]() ����
����![]() ��
��
��3����![]() �ĶԳ���Ϊ��
�ĶԳ���Ϊ��![]() ��
��
![]() �ĶԳ���Ϊ��
�ĶԳ���Ϊ��![]() ��
��
��![]() ��
��
����������ͼ�����£���![]() ʱ��x����ʱ������
ʱ��x����ʱ������![]() ��ֵ��С�Һ���
��ֵ��С�Һ���![]() ��ֵ����
��ֵ����
��![]() ��
��
�����P��������![]() ��0������
��0������![]() =
=![]() ��
��![]() =
=![]() ��
��
��DE=![]() =
=![]() =
=![]()
�ɢٿ�֪��![]() ����DE=
����DE=![]() ��
��
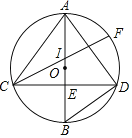
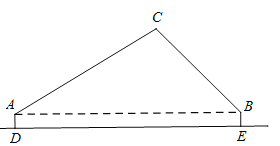
��A����x���ƽ���ߣ���B����y���ƽ���ߣ���ƽ�����ཻ��F��
���F ��������![]() ��
��![]() ����
����
��AF=![]() =
=![]() ��BF=
��BF=![]() =
=![]() ��
��
��AB=![]() =
=![]() ����
����![]() =
=![]() =
=![]() ��
��
��![]() ��ֵֻ���P��λ���йأ�
��ֵֻ���P��λ���йأ�
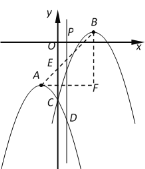

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�