题目内容
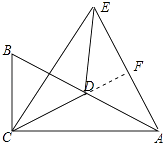
【题目】如图,已知在Rt△ABC中,D是斜边AB的中点,AC=4,BC=2,将△ACD沿直线CD折叠,点A落在点E处,联结AE,那么线段AE的长度等于 . 
【答案】![]()
【解析】解:如图所示:延长CD交AE于F, 由折叠的性质得:CF⊥AE,AC=EC,
∴∠AFC=90°,AF=EF,
∵在Rt△ABC中,∠ACB=90°,
∴AB= ![]() =
= ![]() =2
=2 ![]() ,
,
∵D是斜边AB的中点,
∴CD= ![]() AB=AD,
AB=AD,
∴∠DCA=∠DAC,
∵∠AFC=∠ACB=90°,
∴△AFC∽△BCA,
∴ ![]() ,
,
即 ![]() ,
,
∴AF= ![]() ,
,
∴AE=2AF= ![]() ;
;
所以答案是: ![]() .
.
【考点精析】利用翻折变换(折叠问题)对题目进行判断即可得到答案,需要熟知折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

【题目】如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边的活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡,改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
x(cm) | 10 | 15 | 20 | 25 | 30 |
y(g) | 30 | 20 | 15 | 12 | 10 |

(1)把上表中(x,y)的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点;
(2)观察所画的图象,猜测y与x之间的函数关系,求出函数关系式并加以验证;
(3)当砝码的质量为24g时,活动托盘B与点O的距离是多少cm?
(4)当活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | 1 | 2 | 3 | 4 | 5 | … |
y | … | 0 | ﹣3 | ﹣6 | ﹣6 | ﹣3 | … |
从上表可知,下列说法中正确的有( )
① ![]() =6;②函数y=ax2+bx+c的最小值为﹣6;③抛物线的对称轴是x=
=6;②函数y=ax2+bx+c的最小值为﹣6;③抛物线的对称轴是x= ![]() ;④方程ax2+bx+c=0有两个正整数解.
;④方程ax2+bx+c=0有两个正整数解.
A.1个
B.2个
C.3个
D.4个