题目内容
【题目】已知抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(3,0),C(0,3).
(1)求抛物线的表达式及顶点D的坐标;
(2)如图甲,点P是直线BC上方抛物线上一动点,过点P作y轴的平行线,交直线BC于点E,是否存在一点P,使线段PE的长最大?若存在,求出PE长的最大值;若不存在,请说明理由;
(3)如图乙,过点A作y轴的平行线,交直线BC于点F,连接DA、DB四边形OAFC沿射线CB方向运动,速度为每秒1个单位长度,运动时间为t秒,当点C与点B重合时立即停止运动,设运动过程中四边形OAFC与四边形ADBF重叠部分面积为S,请求出S与t的函数关系式.
【答案】
(1)
解:抛物线的解析式:y=﹣x2+4x﹣3,
∴由y=﹣x2+4x﹣3=﹣(x﹣2)2+1,可知:顶点D的坐标(2,1).
(2)
解:存在.
设直线BC的解析式为:y=kx+b,
则 ![]() ,解得
,解得 ![]() ,
,
∴直线BC的解析式为y=x﹣3,
设P(x,﹣x2+4x﹣3),则F(x,x﹣3),
∴PF=(﹣x2+4x﹣3)﹣(x﹣3)=﹣x2+3x=﹣(m﹣ ![]() )2+
)2+ ![]() ,
,
∴当x= ![]() 时,PE有最大值为
时,PE有最大值为 ![]() .
.
∴存在一点P,使线段PE的长最大,最大值为 ![]() .
.
(3)
解:∵A(1,0)、B(3,0)、D(2,1)、C(0,﹣3),
∴可求得直线AD的解析式为:y=x﹣1;
直线BC的解析式为:y=x﹣3.
∴AD∥BC,且与x轴正半轴夹角均为45°.
∵AF∥y轴,
∴F(1,﹣2),
∴AF=2.
①当0≤t≤ ![]() 时,如答图1﹣1所示.
时,如答图1﹣1所示.

此时四边形AFF′A′为平行四边形.
设A′F′与x轴交于点K,则AK= ![]() AA′=
AA′= ![]() t.
t.
∴S=SAFF′A′=AFAK=2× ![]() t=
t= ![]() t;
t;
②当 ![]() <t≤2
<t≤2 ![]() 时,如答图1﹣2所示.
时,如答图1﹣2所示.
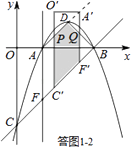
设O′C′与AD交于点P,A′F′与BD交于点Q,
则四边形PC′F′A′为平行四边形,△A′DQ为等腰直角三角形.
∴S=SPC′F′A′﹣S△A′DQ=2×1﹣ ![]() (t﹣
(t﹣ ![]() )2=﹣
)2=﹣ ![]() t2+
t2+ ![]() t+1;
t+1;
③当2 ![]() <t≤3
<t≤3 ![]() 时,如答图1﹣所示.
时,如答图1﹣所示.
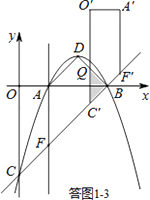
设O′C′与BD交于点Q,则△BC′Q为等腰直角三角形.
∵BC=3 ![]() ,CC′=t,
,CC′=t,
∴BC′=3 ![]() ﹣t.
﹣t.
∴S=S△BC′Q= ![]() (3
(3 ![]() ﹣t)2=
﹣t)2= ![]() t2﹣3
t2﹣3 ![]() t+9.
t+9.
∴综上所述,S与t的函数关系式为:
S= 
【解析】(1)利用待定系数法即可求得抛物线的解析式,然后化为顶点式即可求得顶点的坐标.(2)先求得直线BC的解析式,设P(x,﹣x2+4x﹣3),则F(x,x﹣3),根据PF等于P点的纵坐标减去F点的纵坐标即可求得PF关于x的函数关系式,从而求得P的坐标和PF的最大值;(3)在运动过程中,分三种情形,需要分类讨论,避免漏解.
【考点精析】根据题目的已知条件,利用二次函数的最值的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.

 习题精选系列答案
习题精选系列答案【题目】在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分 组 | 频数 | 频率 |
第一组(0≤x<15) | 3 | 0.15 |
第二组(15≤x<30) | 6 | a |
第三组(30≤x<45) | 7 | 0.35 |
第四组(45≤x<60) | b | 0.20 |

(1)频数分布表中a= , b= , 并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?





