题目内容
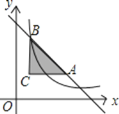
【题目】(10分)如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC.
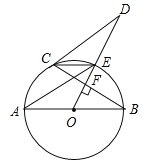
(1)求证:直线CD为⊙O的切线;
(2)若AB=5,BC=4,求线段CD的长.
【答案】(1)证明见试题解析;(2)![]() .
.
【解析】
试题(1)利用圆周角定理结合等腰三角形的性质得出∠OCF+∠DCB=90°,即可得出答案;
(2)利用圆周角定理得出∠ACB=90°,利用相似三角形的判定与性质得出DC的长.
试题解析:(1)连接OC,∵∠CEA=∠CBA,∠AEC=∠ODC,∴∠CBA=∠ODC,又∵∠CFD=∠BFO,∴∠DCB=∠BOF,∵CO=BO,∴∠OCF=∠B,∵∠B+∠BOF=90°,∴∠OCF+∠DCB=90°,∴直线CD为⊙O的切线;
(2)连接AC,∵AB是⊙O的直径,∴∠ACB=90°,∴∠DCO=∠ACB,又∵∠D=∠B,∴△OCD∽△ACB,∵∠ACB=90°,AB=5,BC=4,∴AC=3,∴![]() ,即
,即![]() ,解得;DC=
,解得;DC=![]() .
.

练习册系列答案
相关题目