Question

【题目】在平面直角坐标系xOy中，已知线段a，P为线段a上任意一点，已知图形M，Q为图形M上任意一点，当P，Q两点间的距离最小时，将此时PQ的长度称为图形M与线段a的近点距；当P，Q两点间的距离最大时，将此时PQ的长度称为图形M与线段a的远点距．

根据阅读材料解决下列问题：

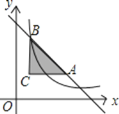
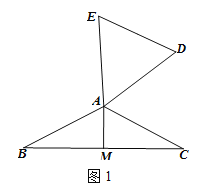
如图1，在平面直角坐标系xOy中，点A的坐标为（﹣2，﹣2），正方形ABCD的对称中心为原点O．

（1）线段AB与线段CD的近点距是　 　，远点距是　 　．

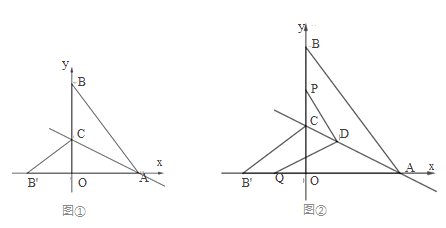
（2）如图2，直线y＝﹣x+6与x轴，y轴分别交于点E，F，则线段EF和正方形ABCD的近点距是　 　，远点距是　 　；

（3）直线y＝x+b（b≠0）与x轴，y轴分别交于点R，S，线段RS与正方形ABCD的近距点是，则b的值是　 　；

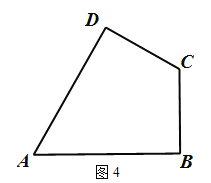
（4）在平面直角坐标系xOy中，有一个矩形GHMN，若此矩形至少有一个顶点在以O为圆心1为半径的圆上，其余各点可能在圆上或圆内，将正方形ABCD绕点O旋转一周，在旋转过程中，它与矩形GHMN的近点距的最小值是　 ，远点距的最大值是　 　．

Answer 1

【答案】（1）4，4；（2），；（3）±8；（4）1，2+1．

【解析】

（1）线段AB与线段CD的近点距是正方形的边长，远点距是正方形的对角线；

（2）如图2中，连接AC，，延长AC交EF于M．解直角三角形求出，，即可解决问题；

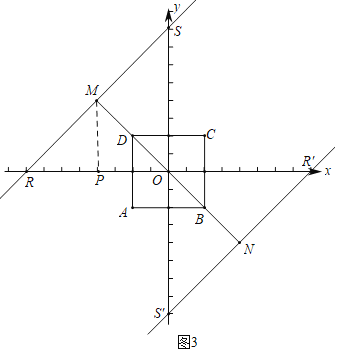
（3）如图3中，设直线BD交直线y＝x+b于M，N．由题意当DM＝BN＝2时，线段RS与正方形ABCD的近距点是2，作MP⊥OR于P，由△OPM是等腰直角三角形，OM＝4，求出点M的坐标，再利用待定系数法即可解决问题；

（4）如图4中，作正方形ABCD的外接圆与内切圆．利用图象法解决问题即可．

（1）线段AB与线段CD的近点距是正方形的边长＝4，

远点距是正方形的对角线＝4．

故答案为4，4．

（2）如图2中，连接AC，，延长AC交EF于M．

直线y＝﹣x+6与x轴、y轴的交点坐标分别是：E(6，0)，F(0，6)，

∵四边形ABCD是正方形，且OE＝OF＝6，

∴OM平分∠EOF，

∴OM⊥EF，，

∴ME＝MF，

∴OM＝EF＝3，

∵OC＝OA＝2，

∴AM＝5，CM＝，

∴

∴线段EF和正方形ABCD的近点距是，远点距是．

故答案为：，．

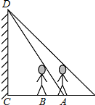
（3）如图3中，设直线BD交直线y＝x+b于M，N．

由题意当DM＝BN＝2时，线段RS与正方形ABCD的近距点是2，

作MP⊥OR于P，

∵△OPM是等腰直角三角形，OM＝4，

∴PM＝OP＝4，

∴M（﹣4，4），同法可得N（4，﹣4），

把M（﹣4，4），代入y＝x+b得到b＝8，

把N′（4，﹣4），代入y＝x+b得到b＝﹣8，

故答案为：±8．

（4）如图4中，作正方形ABCD的外接圆与内切圆．

　

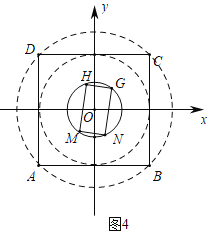
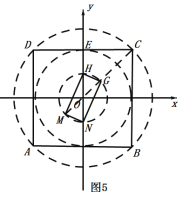
观察图象可知将正方形ABCD绕点O旋转一周，在旋转过程中，它与矩形GHMN的近点距的最小值是：1，远点距的最大值是：，

故答案为：1，．