题目内容
【题目】如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒. 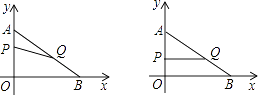
(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△AOB相似?
(3)当t为何值时,△APQ的面积为 ![]() 个平方单位?
个平方单位?
【答案】
(1)解:设直线AB的解析式为y=kx+b,
由题意,得 ![]() ,
,
解得 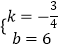 ,
,
所以,直线AB的解析式为y=﹣ ![]() x+6
x+6
(2)解:由AO=6,BO=8得AB=10,
所以AP=t,AQ=10﹣2t,
① 当∠APQ=∠AOB时,△APQ∽△AOB.
所以 ![]() =
= ![]() ,
,
解得t= ![]() (秒),
(秒),
②当∠AQP=∠AOB时,△AQP∽△AOB.
所以 ![]() =
= ![]() ,
,
解得t= ![]() (秒);
(秒);
∴当t为 ![]() 秒或
秒或 ![]() 秒时,△APQ与△AOB相似
秒时,△APQ与△AOB相似
(3)解:过点Q作QE垂直AO于点E.
在Rt△AOB中,sin∠BAO= ![]() =
= ![]() ,
,
在Rt△AEQ中,QE=AQsin∠BAO=(10﹣2t) ![]() =8﹣
=8﹣ ![]() t,
t,
S△APQ= ![]() APQE=
APQE= ![]() t(8﹣
t(8﹣ ![]() t),
t),
=﹣ ![]() t2+4t=
t2+4t= ![]() ,
,
解得t=2(秒)或t=3(秒).
∴当t为2秒或3秒时,△APQ的面积为 ![]() 个平方单位
个平方单位
【解析】(1)设直线AB的解析式为y=kx+b,解得k,b即可;(2)由AO=6,BO=8得AB=10,①当∠APQ=∠AOB时,△APQ∽△AOB利用其对应边成比例解t.②当∠AQP=∠AOB时,△AQP∽△AOB利用其对应边成比例解得t.(3)过点Q作QE垂直AO于点E.在Rt△AEQ中,QE=AQsin∠BAO=(10﹣2t) ![]() =8﹣
=8﹣ ![]() t,再利用三角形积解得t即可.
t,再利用三角形积解得t即可.

 名校课堂系列答案
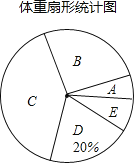
名校课堂系列答案【题目】某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:
体重频数分布表
组边 | 体重(千克) | 人数 |
A | 45≤x<50 | 12 |
B | 50≤x<55 | m |
C | 55≤x<60 | 80 |
D | 60≤x<65 | 40 |
E | 65≤x<70 | 16 |
(1)填空:①m=__(直接写出结果);
②在扇形统计图中,C组所在扇形的圆心角的度数等于__度;
(2)如果该校九年级有1000名学生,请估算九年级体重低于60千克的学生大约有多少人?