Question

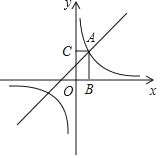
【题目】如图，已知点A（a，3）是一次函数y1＝x+1与反比例函数y2＝的图象的交点．（1）求反比例函数的解析式；（2）在y轴的右侧，当y1＞y2时，直接写出x的取值范围；（3）求点A与两坐标轴围成的矩形OBAC的面积．

Answer 1

【答案】（1）y2＝；（2）x＞2；（3）点A与两坐标轴围成的矩形OBAC的面积是6．

【解析】

（1）将点A的坐标代入一次函数的解析式，求得a值后代入反比例函数求得b的值后即可确定反比例函数的解析式；

（2）y1＞y2时y1的图象位于y2的图象的上方，据此求解．

（3）根据反比例函数k值的几何意义即可求解．

解：（1）将A（a，3）代入一次函数y1＝x+1得a+1＝3，

解得a＝2，

∴A（2，3），

将A（2，3）代入反比例函数得，解得k＝6，

∴

（2）∵A（2，3），y1＝x+1，

∴在y轴的右侧，当y1＞y2时，x的取值范围是x＞2；

（3）∵k＝6，

∴点A与两坐标轴围成的矩形OBAC的面积是6．