Question

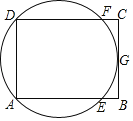
【题目】（11·钦州）把一张矩形纸片ABCD按如图方式折叠，使顶点B和顶点D重合，折痕为EF．若BF＝4，FC＝2，则∠DEF的度数是_ ．

Answer 1

【答案】60º

【解析】

根据折叠的性质得到DF=BF=4，∠BFE=∠DFE，在Rt△DFC中，根据含30°的直角三角形三边的关系得到∠FDC=30°，则∠DFC=60°，所以有∠BFE=∠DFE=（180°-60°）÷2，然后利用两直线平行内错角相等得到∠DEF的度数．

解：∵矩形纸片ABCD按如图方式折叠，使顶点B和顶点D重合，折痕为EF，

∴DF=BF=4，∠BFE=∠DFE，

在Rt△DFC中，FC=2，DF=4，

∴∠FDC=30°，

∴∠DFC=60°，

∴∠BFE=∠DFE=（180°-60°）÷2=60°，

∴∠DEF=∠BFE=60°．

故答案为60．