题目内容
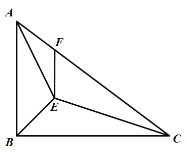
【题目】如图一所示,△ABC是等腰直角三角形,其中∠BAC=90°,D是AB边上的一点,连接CD,过A作AE⊥CD,E为垂足,AF⊥AE,且AF=AE.连接FB
(1)求证:CE=FB;
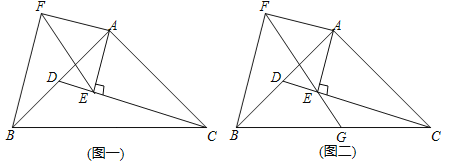
(2)如图二,延长FE交BC于G点,如果G点正好为BC的中点,求证:![]() EG+EA=FB.
EG+EA=FB.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由“HL”可证Rt△AEC≌Rt△AFB,可得CE=FB;
(2)过点G作GH⊥EG,交CD于H,连接AG,由全等三角形的性质可得AF=AE,∠BAF=∠CAE,可求∠AFE=∠AEF=∠GEH=45°,可得EH=![]() EG,由“SAS”可证△AEG≌△CHG,可得AE=CH,即可得结论.
EG,由“SAS”可证△AEG≌△CHG,可得AE=CH,即可得结论.
证明:(1)∵AE⊥CD,AF⊥AE,
∴∠AFB=∠AEC=90°,
∵AF=AE,AB=AC,
∴Rt△AEC≌Rt△AFB(HL)
∴CE=FB;
(2)如图(二),过点G作GH⊥EG,交CD于H,连接AG,
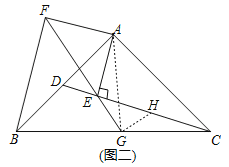
∵Rt△AEC≌Rt△AFB,
∴AF=AE,∠BAF=∠CAE,
∵∠CAE+∠DAE=90°,
∴∠BAF+∠DAE=90°,
∴∠FAE=90°,且AF=AE,
∴∠AFE=∠AEF=45°,
∴∠GEH=45°,且GH⊥EG
∴∠GEH=∠GHE=45°,
∴EG=GH,
∴EH=![]() EG,
EG,
∵AB=AC,∠BAC=90°,点G是BC中点,
∴AG=GC,AG⊥GC,
∴∠AGC=∠EGH=90°,
∴∠AGE=∠CGH,EG=GH,AG=GC,
∴△AEG≌△CHG(SAS)
∴AE=CH,
∴BF=CE=EH+HC=![]() EG+AE.
EG+AE.

练习册系列答案
相关题目