题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,以点
上,以点![]() 为圆心作⊙
为圆心作⊙![]() .当⊙
.当⊙![]() 恰好同时与边
恰好同时与边![]() ,
,![]() 相切时,⊙
相切时,⊙![]() 的半径长为________.
的半径长为________.

【答案】![]()
【解析】
作AH⊥BC于H,DE⊥BC于E,DF⊥AC于F,连接CD,如图,设⊙D的半径为r,先利用等腰三角形的性质得BH=CH=![]() BC=5,则利用勾股定理可计算出AH=12,再根据切线的性质得DE=DF=r,然后根据三角形面积公式得到
BC=5,则利用勾股定理可计算出AH=12,再根据切线的性质得DE=DF=r,然后根据三角形面积公式得到![]() AHBC=
AHBC=![]() DEBC+
DEBC+![]() DFAC,即
DFAC,即![]() ×10r+
×10r+![]() ×13×r=
×13×r=![]() ×10×12,,再解关于r的方程即可.
×10×12,,再解关于r的方程即可.
作AH⊥BC于H,DE⊥BC于E,DF⊥AC于F,连接CD,如图,设 D的半径为r,
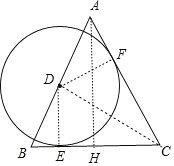
∵AB=AC,AH⊥BC,
∴BH=CH=![]() BC=5,
BC=5,
在Rt△ABH中,根据勾股定理求得AH=12,
∵⊙D同时与边AC、BC相切,
∴DE=DF=r,
∵S△ABC=S△ADC+S△DBC,
∴![]() AHBC=
AHBC=![]() DEBC+
DEBC+![]() DFAC,
DFAC,
即![]() ×10r+
×10r+![]() ×13×r=
×13×r=![]() ×10×12,
×10×12,
∴r=![]() ,
,
即当 D恰好同时与边AC、BC相切时,此时 D的半径长为![]() .
.
故答案为: ![]() .
.

练习册系列答案
相关题目










