��Ŀ����
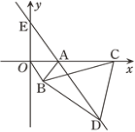
����Ŀ����ͼ����������������A��B��C����ʾ�����ֱ��ǩ�4����2��3����ش�
��1����ʹC��B����ľ�����A��B����ľ�����ȣ����轫��C�����ƶ�_____����λ��
��2����A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶����˶�t���ӹ���
����A��B��C��ʾ�����ֱ���_____��_____��_____ ���ú�t�Ĵ���ʽ��ʾ����
������B���C֮��ľ����ʾΪd1����A���B֮��ľ����ʾΪd2�����ʣ�d1��d2��ֵ�Ƿ�����ʱ��t�ı仯���ı䣿���仯����˵�����ɣ������䣬�����d1��d2ֵ��
![]()
���𰸡� 3��7 ��4��t ��2+2t ��2+2t
�������������������1����AB=2��������ἴ�ɵó���C�����ƶ��ľ��룻
��2���ٽ��·��=ʱ����ٶ�д���𰸣�
�������d1=3t+5��d2=3t+2���Ӷ��ó�d1��d2=2��
�����������1���������֪��A��B����ľ���Ϊ2��B�㡢C���ʾ�����ֱ�Ϊ����2��3��
���Ե�C��B����ľ�����A��B����ľ������ʱ���轫��C�����ƶ�3����7����λ��
�ʴ��ǣ�3��7��
��2���ٵ�A��ʾ�����ǩ�4��t����B��ʾ�����ǩ�2+2t����C����ʾ������3+5t��
�ʴ��ǣ���4��t����2+2t��3+5t��
��d1��d2��ֵ������ʱ��t�ı仯���ı䣬��ֵ��3���������£�
�ߵ�A����ÿ��1����λ���ٶ������˶�����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶���
��d1=3t+5��d2=3t+2��
��d1��d2=��3t+5������3t+2��=3��

 ��ҵ����ϵ�д�
��ҵ����ϵ�д�����Ŀ��������ijͬѧ�Զ���ʽ��x2��4x+2����x2��4x+6��+4������ʽ�ֽ�Ĺ��̣�
�⣺��x2��4x=y
ԭʽ=��y+2����y+6��+4 ����һ����
=y2+8y+16 ���ڶ�����
=��y+4��2����������
=��x2��4x+4��2�����IJ���
�ش��������⣺
��1����ͬѧ�ڶ�������������������ʽ�ֽ��_______��
A����ȡ����ʽ |
B��ƽ���ʽ |
C�������͵���ȫƽ����ʽ |
D�����������ȫƽ����ʽ |
��2����ͬѧ��ʽ�ֽ�Ľ���Ƿף�________�����������������������������������ף���ֱ��д����ʽ�ֽ�������_________ ��
��3������ģ�����Ϸ������ԶԶ���ʽ��x2��2x����x2��2x+2��+1������ʽ�ֽ⣮