题目内容
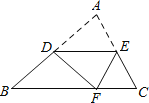
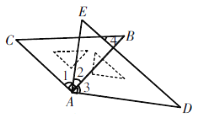
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F,H是边BC的中点,连接 DH与 BE相交于点 G,若GE=3,则BF=_____.
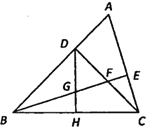
【答案】6
【解析】
求出 BG=GC,求出∠EGC=∠ECG,推出 CE=GE,进而利用等腰三角形的性质和全等三角形的判定和性质解答即可.
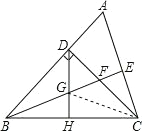
解:连接 CG,
∵BD=DC,H 为 BC 中点,
∴DH 为 BC 垂直平分线,
∴BG=CG,
∴∠ABE=∠CBE=∠GCB,
∵∠ABC=45°,∠ABE=∠CBE,
∴∠EGC=∠CBE+∠GCB=45°,
∵∠GEC=90°,
∴∠ECG=45°=∠EGC,
∴GE=CE=3.
∵BE 平分∠ABC,且 BE⊥AC 于点 E,
∴AE=EC=3,
∴AC=6,
∵CD⊥AB,
∴∠CDB=90°,
∵∠ABC=45°,
∴∠DCB=45°=∠DBC,
∴BD=DC,
在△BDF 和△CEF 中,
∵∠BDC=∠BEC=90°,∠DFB=∠EFC,
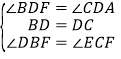 ∴∠DBF=∠ECF, 在△BDF 和△CDA 中
∴∠DBF=∠ECF, 在△BDF 和△CDA 中
∴△BDF≌△CDA(ASA),
∴BF=AC=6; 故答案为:6;

练习册系列答案
相关题目