题目内容
【题目】阅读下列材料,然后解决问题:和、差、倍、分等问题中有着广泛的应用,截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
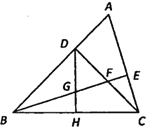
(1)如图1,在△ABC中,若 AB=12,AC=8,求 BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使 DE=AD,再连接 BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线 AD的取值范围是_______.
问题解决:
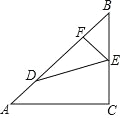
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,CD上的两点,且∠EAF=![]() ∠BAD,求证:BE+DF=EF.
∠BAD,求证:BE+DF=EF.
问题拓展:
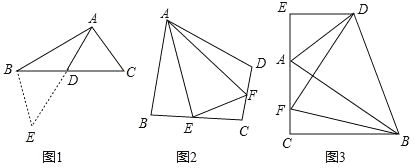
(3)如图3,在△ABC中,∠ACB=90°,∠CAB=60°,点D是△ABC 外角平分线上一点,DE⊥AC交 CA延长线于点E,F是 AC上一点,且DF=DB.
求证:AC﹣AE=![]() AF.
AF.
【答案】(1)2<AD<10;(2)证明见解析;(3)证明见解析.
【解析】
(1)延长 AD 到点 E 使 DE=AD,连接 BE,证明△ADC≌△EDB,根据全等三角形的性质得到 BE=AC,根据三角形三边关系计算;
(2)延长 CB 到 G,使 BG=DF,证明△ABG≌△ADF,根据全等三角形的性质得到 AG=AF,∠GAB=∠FAD,证明△AEG≌△AEF,根据全等三角形的性质证明;
(3)作 DH⊥AB 于 H,在 AB 上截取 BR=AF,分别证明 Rt△DEF≌Rt△DHB,
 △DAF≌△DRB,根据全等三角形的性质证明.
△DAF≌△DRB,根据全等三角形的性质证明.
解:(1)延长 AD 到点E使 DE=AD,连接 BE,
在△ADC 和△EDB中,

∴△ADC≌△EDB(SAS),
∴BE=AC=8,
AB﹣BE<AE<AB+BE,即21﹣8<2AD<12+8,
∴2<AD<10,
故答案为:2<AD<10;
(2)证明:延长 CB 到 G,使 BG=DF,
∵∠ABC+∠ADC=180°,∠ABC+∠ABG=180°,
∴∠ADC=∠ABG,
在△ABG 和△ADF 中,

∴△ABG≌△ADF(SAS),
∴AG=AF,∠GAB=∠FAD,
∵∠EAF= ![]() ∠BAD,
∠BAD,
∴∠FAD+∠BAE=∠GAB+∠BAE=![]() ∠BAD,
∠BAD,
∴∠GAE=∠FAE,
在△AEG 和△AEF 中,

∴△AEG≌△AEF(SAS),
∴EF=GE,
∴EF=BE+BG=BE+DF;

(3)证明:作 DH⊥AB 于 H,在 AB 上截取 BR=AF,
∵∠CAB=60°,∠ACB=90°,
∴∠ABC=30°,
∴AB=2AC,
∵点 D 是△ABC 外角平分线上一点,DE⊥AC,DH⊥AB,
∴DE=DH,AH=AE,
在 Rt△DEF 和 Rt△DHB 中,
![]()
∴Rt△DEF≌Rt△DHB(HL)
∴∠DFA=∠DBA,
在△DAF 和△DRB 中,

∴△DAF≌△DRB(SAS)
∴DA=DR,
∴AH=HR=AE= ![]() AR,
AR,
∵AF=BR=AB﹣AR=2AC﹣2AE
∴AC﹣AE=![]() AF.
AF.

【题目】问题情景:
如图,在直角坐标系xOy中,点A、B为二次函数y=ax2(a>0)图象上的两点,且点A、B的横坐标分别为m、n(m>n>0),连接OA、AB、OB.设△AOB的面积为S时,解答下列问题: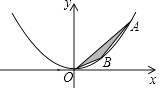
(1)探究:当a=1时,
mn | m﹣n | S | |
m=3,n=1 | 3 | 2 | |
m=5,n=2 | 10 | 3 |
当a=2时,
2mn | m﹣n | S | |
m=3,n=1 | 6 | 2 | |
m=5,n=2 | 20 | 3 |
(2)归纳证明:对任意m、n(m>n>0),猜想S=(用a,m,n表示),并证明你的猜想.
(3)拓展应用:
若点A、B的横坐标分别为m、n(m>0>n),其它条件不变时,△AOB的面积S=(用a,m,n表示).