题目内容
【题目】定义:若
则称
与
是关于1的平衡数。
(1)5与______是关于1的平衡数；
(2)
与________是关于1的平衡数(用含
的代数式表示)；
(3)若
判断与是否是关于1的平衡数,并说明理由。
【答案】(1)-3，（2）2x-5；（3）不是，理由见解析.
【解析】
（1）由平衡数的定义可求得答案；
（2）由平衡数的定义可求得答案；
（3）计算a+b是否等于1即可．
（1）设5的关于1的平衡数为a，则5+a=2，解得a=-3，
∴5与-3是关于1的平衡数，
（2）设7-2x的关于1的平衡数为b，则7-2x+b=2，解得b=2-（7-2x）=2x-5，
∴7-2x与2x-5是关于1的平衡数，
（3）a与b不是关于1的平衡数，理由如下：
∵
，
∴a+b=2x2-3（x2+x）+4-3x+6x+x2=2x2-3x2-3x+4-3x+6x+x2=6x+4≠2，
∴a与b不是关于1的平衡数．
练习册系列答案
阅读快车系列答案
相关题目
【题目】问题情景：
如图，在直角坐标系xOy中，点A、B为二次函数y=ax2（a＞0）图象上的两点，且点A、B的横坐标分别为m、n（m＞n＞0），连接OA、AB、OB．设△AOB的面积为S时，解答下列问题：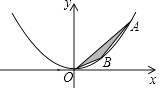
（1）探究：当a=1时，
mn | m﹣n | S | |
m=3，n=1 | 3 | 2 | |
m=5，n=2 | 10 | 3 |
当a=2时，
2mn | m﹣n | S | |
m=3，n=1 | 6 | 2 | |
m=5，n=2 | 20 | 3 |
（2）归纳证明：对任意m、n（m＞n＞0），猜想S=（用a，m，n表示），并证明你的猜想．
（3）拓展应用：
若点A、B的横坐标分别为m、n（m＞0＞n），其它条件不变时，△AOB的面积S=（用a，m，n表示）．
