题目内容
【题目】某一小球以一定的初速度开始向前滚动，并且均匀减速，小球滚动的速度v（单位：米/秒）与时间x（单位：秒）之间关系的部分数据如表一：
表一：
时间x（秒） | 0 | 1 | 2 | 2.5 | 3 | … |
速度v（米/秒） | 8 | 6 | 4 | 3 | 2 | … |
（1）根据表一的信息，请在表二中填写滚动的距离s（单位：米）的对应值，（提示：本题中，s=
×x， =
，其中，v0表示开始时的速度，vx表示x秒时的速度．）
表二：
时间x（秒） | 0 | 1 | 2 | 3 | … |
距离s（米） | 0 | … |
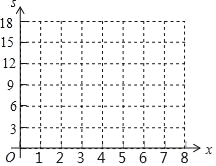
（2）根据表二中的数据在给出的平面坐标系中画出相应的点；
（3）选择适当的函数表示s与x之间的关系，求出相应的函数解析式；
（4span>）当s=13.75时，求滚动时间x．
【答案】（1）见解析；（2）见解析；（3）函数解析式为：s=﹣x2+8x；（4）x=2.5．
【解析】分析：（1）首先求出
的值，进而分别得出s的值，即可得出答案；
（2）利用（1）中所求描出各点即可；
（3）利用待定系数法确定函数关系式即可；
（4）利用s=13.75，进而代入（3）中解析式进而得出答案．
详解：（1）当x=1时， =
=7，则s=7×1=7；
当x=2时， =
=6，则s=2×6=12；
当x=3时， =
=5，则s=3×5=15；
时间x（秒） | 0 | 1 | 2 | 3 | … |
距离s（米） | 0 | 7 | 12 | 15 | … |
（2）如图所示：
；
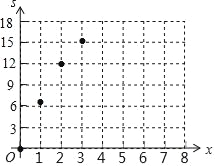（3）由图象可得s是x的二次函数，设s=ax2+bx，把（1，7，（2，12）代入可得：
，
解得：
，
故相应的函数解析式为：s=﹣x2+8x；
（4）当s=13.75时，则﹣x2+8x=13.75，
解得：x1=2.5，x2=5.5，
∵0≤x≤4，
∴x=2.5．
练习册系列答案
相关题目
