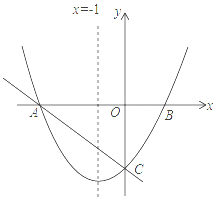题目内容
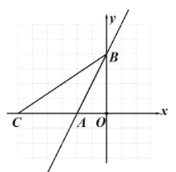
【题目】如图,一次函数y=2x+4的图象分别与x轴,y轴教育点A、点B、点C为x轴一动点。
(1)求A,B两点的坐标;
(2)当ΔABC的面积为6时,求点C的坐标;
(3)平面内是否存在一点D,使四边形ACDB使菱形,若存在,请直接写出点D的坐标;若不存在,请说明理由。
【答案】(1)点A(-2,0),B(0,4);(2)点C(-5,0)或(1,0);(3)D (-![]() ,4)或(
,4)或(![]() ,4).
,4).
【解析】
(1) 利用坐标轴上点的特点求解即可得出结论;
(2) 根据△AOB的面积,可得出点C的坐标;
(3)根据勾股定理求出AB的长,再利用菱形的性质可得结果,分两种情况讨论.
(1)当x=0,y=4
当y=0,x=-2
∴点A(-2,0),B(0,4)
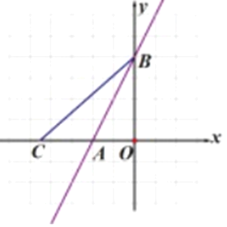
(2)因为A(-2,0),B(0,4)
∴OA=2,OB=4
ΔABC的面积为![]()
因为ΔABC的面积为6
∴AC=3
∵A(-2,0)
∴点C(-5,0)或(1,0)
(3)存在,理由:①如图:点C再A点左侧,
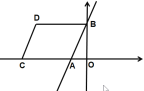
∵A(-2,0),B(0,4), ∴AB=![]() ,∵四边形ACDB为菱形,∴AC=AB=
,∵四边形ACDB为菱形,∴AC=AB=![]() ,∵AC
,∵AC![]() BD, ∴AC=BD=AB=
BD, ∴AC=BD=AB=![]() ,∴D(-
,∴D(-![]() ,4);
,4);
②如图:点C再A点右侧,
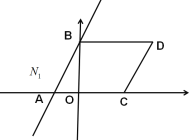
∵A(-2,0),B(0,4), ∴AB=![]() ,∵四边形ACDB为菱形,∴AC=AB=
,∵四边形ACDB为菱形,∴AC=AB=![]() ,∵AC
,∵AC![]() BD, ∴AC=BD=AB=
BD, ∴AC=BD=AB=![]() ,∴D(
,∴D(![]() ,4);综上所述:D点的坐标为(-
,4);综上所述:D点的坐标为(-![]() ,4),(
,4),(![]() ,4)
,4)

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案【题目】某一小球以一定的初速度开始向前滚动,并且均匀减速,小球滚动的速度v(单位:米/秒)与时间x(单位:秒)之间关系的部分数据如表一:
表一:
时间x(秒) | 0 | 1 | 2 | 2.5 | 3 | … |
速度v(米/秒) | 8 | 6 | 4 | 3 | 2 | … |
(1)根据表一的信息,请在表二中填写滚动的距离s(单位:米)的对应值,(提示:本题中,s=![]() ×x,
×x,![]() =
=![]() ,其中,v0表示开始时的速度,vx表示x秒时的速度.)
,其中,v0表示开始时的速度,vx表示x秒时的速度.)
表二:
时间x(秒) | 0 | 1 | 2 | 3 | … |
距离s(米) | 0 | … |
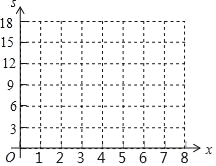
(2)根据表二中的数据在给出的平面坐标系中画出相应的点;
(3)选择适当的函数表示s与x之间的关系,求出相应的函数解析式;
(4span>)当s=13.75时,求滚动时间x.
【题目】如图1是一个长时间没有使用的弹簧测力计,经刻度盘,指针,吊环,挂钩等个部件都齐全,但小明还是对其准确程度表示怀疑,于是他利用数学知识对这个弹簧测力计进行检验。下表是他记录的数据的一部分:
弹簧所挂物体的质量(单位:㎏) | 0 | 0.1 | 0.2 | 0.3 | 0.4 |
弹簧的长度(单位cm) | 12 | 12.5 | 13 | 13.5 | 14 |
在整理数据的过程中,他发现在所挂物体的质量不超过1㎏时,弹簧的长度与弹簧所挂物体的质量之间存在着函数关系,于是弹簧所挂物体的质量x㎏,弹簧的长度为ycm。
(1)请你利用如图2的坐标系,描点并画出函数的大致图象。
(2)根据函数图象,猜想y与x之间是怎样的函数,求出对应的函数解析式。
(3)你认为该测力计是否可以正常使用,如果可以,请你求出所挂物体的质量为1㎏时,弹簧的长度;如果不可以,请说明理由。

【题目】为了解高中学生每月用掉中性笔笔芯的情况,随机抽查了30名高中学生进行调查,并将调查的数据制成如下的表格:
月平均用中性笔笔芯(根) | 4 | 5 | 6 | 7 | 8 | 9 |
被调查的学生数 | 7 | 4 | 9 | 5 | 2 | 3 |
请根据以上信息,解答下列问题:
(1)被调查的学生月平均用中性笔笔芯数大约________根;
(2)被调查的学生月用中性笔笔芯数的中位数为________根,众数为________根;
(3)根据样本数据,若被调查的高中共有1000名学生,试估计该校月平均用中性笔笔芯数9根的约多少人?