题目内容
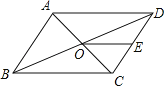
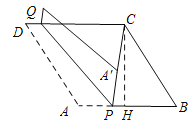
【题目】如图,在菱形![]() 中,
中, ![]() ,
, ![]() 是
是![]() 上一点,
上一点,![]() ,
, ![]() 是
是![]() 边上一动点,将四边形
边上一动点,将四边形![]() 沿宜线
沿宜线![]() 折叠,
折叠,![]() 的对应点
的对应点![]() .当
.当![]() 的长度最小时,则
的长度最小时,则![]() 的长为( )
的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由A′P=6可知点A′在以P为圆心以PA′为半径的弧上,故此当C,P,A′在一条直线上时,CA′有最小值,过点C作CH⊥AB,垂足为H,先求得BH、HC的长,则可得到PH的长,然后再求得PC的长,最后依据折叠的性质和平行线的性质可证明△CQP为等腰三角形,则可得到QC的长.
由A′P=6可知点A′在以P为圆心以PA′为半径的弧上,故此当C,P,A′在一条直线上时,CA′有最小值,过点C作CH⊥AB,垂足为H.
在Rt△BCH中,∠B=60°,BC=16,则
BH=![]() BC=8,CH=
BC=8,CH=![]() =8
=8![]() .
.
∴PH=2.
在Rt△CPH中,依据勾股定理可知:PC=![]() =14.
=14.
由翻折的性质可知:∠APQ=∠A′PQ.
∵DC∥AB,
∴∠CQP=∠APQ.
∴∠CQP=∠CPQ.
∴QC=CP=14.
故选:D.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
【题目】某一小球以一定的初速度开始向前滚动,并且均匀减速,小球滚动的速度v(单位:米/秒)与时间x(单位:秒)之间关系的部分数据如表一:
表一:
时间x(秒) | 0 | 1 | 2 | 2.5 | 3 | … |
速度v(米/秒) | 8 | 6 | 4 | 3 | 2 | … |
(1)根据表一的信息,请在表二中填写滚动的距离s(单位:米)的对应值,(提示:本题中,s=![]() ×x,
×x,![]() =
=![]() ,其中,v0表示开始时的速度,vx表示x秒时的速度.)
,其中,v0表示开始时的速度,vx表示x秒时的速度.)
表二:
时间x(秒) | 0 | 1 | 2 | 3 | … |
距离s(米) | 0 | … |
(2)根据表二中的数据在给出的平面坐标系中画出相应的点;
(3)选择适当的函数表示s与x之间的关系,求出相应的函数解析式;
(4span>)当s=13.75时,求滚动时间x.