题目内容
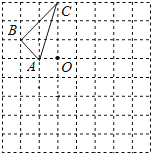
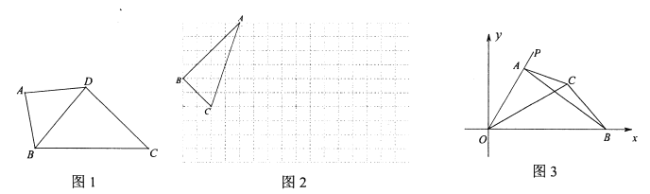
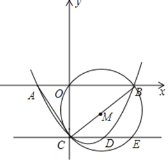
【题目】已知抛物线y=a(x﹣1)(x﹣3)(a<0)的顶点为A,交y轴交于点C,过C作CB∥x轴交抛物线于点B,过点B作直线l⊥x轴,连结OA并延长,交l于点D,连结OB.

(1)当a=﹣1时,求线段OB的长.
(2)是否存在特定的a值,使得△OBD为等腰三角形?若存在,请写出求a值的计算过程;若不存在,请说明理由.
(3)设△OBD的外心M的坐标为(m,n),求m与n的数量关系式.
【答案】(1)5;(2)a=﹣1或﹣![]() ;(3)m=3n2+2
;(3)m=3n2+2
【解析】
由y=a(x﹣1)(x﹣3)=a(x2﹣4x+3),可得点C(0,3a)、对称轴为:x=2,点B(4,3a),点A(2,﹣a),点D(4,﹣2a);
(1)把a=-1代入求得点B(4,﹣3),继而可得OB长;
(2)分OD=OB、OD=BD、OB=BD三种情况,分别求解即可;
(3)线段OD的中垂线的表达式为:y=![]() x﹣a﹣
x﹣a﹣![]() …①,线段BD的中垂线的表达式为:y=
…①,线段BD的中垂线的表达式为:y=![]() a…②,联立①②并解得:x=
a…②,联立①②并解得:x=![]() a2+2=m,y=
a2+2=m,y=![]() a=n,即可求解.
a=n,即可求解.
y=a(x﹣1)(x﹣3)=a(x2﹣4x+3),
当x=0时,y=3a,
所以点C(0,3a)、
函数的对称轴为:x=2,
所以点B(4,3a),
当x=2时,y= a(2﹣1)(2﹣3)=-a,
所以点A(2,﹣a),
设OA的解析式为y=kx,
把A(-2,a)代入,得a=-2k,得k=![]() ,
,
所以直线OA:y=![]() x,
x,
当x=4时,y=-2a,
所以点D(4,﹣2a);
(1)当a=-1时,点B(4,﹣3),故OB=![]() =5;
=5;
(2)OD2=16+4a2,OB2=16+9a2,BD2=25a2,
①当OD=OB时,即16+4a2=16+9a2,解得:a=0(舍去);
②当OD=BD时,同理可得:a=﹣![]() 或a=
或a=![]() (正值舍去);
(正值舍去);
③当OB=BD时,同理可得:a=﹣1或a=1(正值舍去);
综上,a=﹣1或﹣![]() ;
;
(3)线段OD的函数表达式为:y=﹣![]() ax,直线OD的中点为点A(2,﹣a),
ax,直线OD的中点为点A(2,﹣a),
则线段OD的中垂线的表达式为:y=![]() x+b,
x+b,
将点A(2,﹣a)代入上式得:-a=![]() +b,
+b,
解得:b=-a-![]() ,
,
所以线段OD的中垂线的表达式为:y=![]() x﹣a﹣
x﹣a﹣![]() …①,
…①,
线段BD的中垂线的表达式为:y=![]() a…②,
a…②,
联立①②并解得:x=![]() a2+2=m,y=
a2+2=m,y=![]() a=n,
a=n,
故m=3n2+2.

【题目】函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索.画函数![]() 的图象,经历分析解析式、列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数
的图象,经历分析解析式、列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数![]() 和
和![]() 的图象如图所示.
的图象如图所示.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣6 | ﹣4 | ﹣2 | 0 | ﹣2 | ﹣4 | ﹣6 | … |
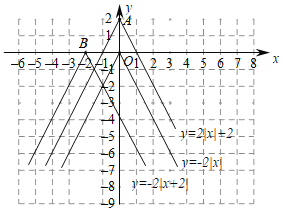
(1)观察发现:三个函数的图象都是由两条射线组成的轴对称图形;三个函数解折式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.写出点A,B的坐标和函数![]() 的对称轴.
的对称轴.
(2)探索思考:平移函数![]() 的图象可以得到函数
的图象可以得到函数![]() 和
和![]() 的图象,分别写出平移的方向和距离.
的图象,分别写出平移的方向和距离.
(3)拓展应用:在所给的平面直角坐标系内画出函数![]() 的图象.若点
的图象.若点![]() 和
和![]() 在该函数图象上,且
在该函数图象上,且![]() ,比较
,比较![]() ,
,![]() 的大小.
的大小.