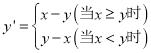题目内容
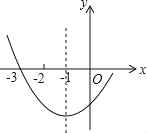
【题目】函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索.画函数![]() 的图象,经历分析解析式、列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数
的图象,经历分析解析式、列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数![]() 和
和![]() 的图象如图所示.
的图象如图所示.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣6 | ﹣4 | ﹣2 | 0 | ﹣2 | ﹣4 | ﹣6 | … |
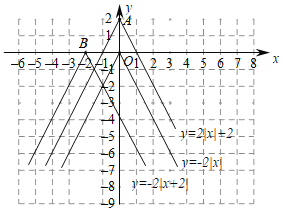
(1)观察发现:三个函数的图象都是由两条射线组成的轴对称图形;三个函数解折式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.写出点A,B的坐标和函数![]() 的对称轴.
的对称轴.
(2)探索思考:平移函数![]() 的图象可以得到函数
的图象可以得到函数![]() 和
和![]() 的图象,分别写出平移的方向和距离.
的图象,分别写出平移的方向和距离.
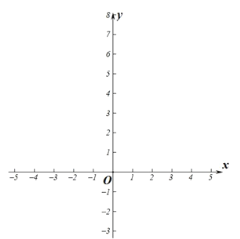
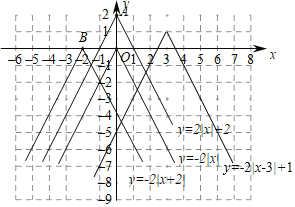
(3)拓展应用:在所给的平面直角坐标系内画出函数![]() 的图象.若点
的图象.若点![]() 和
和![]() 在该函数图象上,且
在该函数图象上,且![]() ,比较
,比较![]() ,
,![]() 的大小.
的大小.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)根据图形即可得到结论;
(2)根据函数图形平移的规律即可得到结论;
(3)根据函数关系式可知将函数![]() 的图象向上平移1个单位,再向右平移3个单位得到函数
的图象向上平移1个单位,再向右平移3个单位得到函数![]() 的图象.根据函数的性质即可得到结论.
的图象.根据函数的性质即可得到结论.
解:(1)![]() ,
,![]() ,函数
,函数![]() 的对称轴为
的对称轴为![]() ;
;
(2)将函数![]() 的图象向上平移2个单位得到函数
的图象向上平移2个单位得到函数![]() 的图象;
的图象;
将函数![]() 的图象向左平移2个单位得到函数
的图象向左平移2个单位得到函数![]() 的图象;
的图象;
(3)将函数![]() 的图象向上平移1个单位,再向右平移3个单位得到函数
的图象向上平移1个单位,再向右平移3个单位得到函数![]() 的图象.
的图象.
所画图象如图所示,当![]() 时,
时,![]() .
.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目