ƒøƒ⁄»ð
°æƒø°ø
£®“—”–æ≠—È£©
Œ“√«“—æ≠—–æøπ˝◊˜“ª∏ˆ‘≤æ≠π˝¡Ω∏ˆ“—÷™µ„£¨“≤—–æøπ˝◊˜“ª∏ˆ‘≤”Γ—÷™Ω«µƒ¡ΩÃı±þ∂ºœý«–£¨≥þπÊ◊˜Õº»ÁÕºÀ˘ æ£∫
£®«®“∆æ≠—È£©
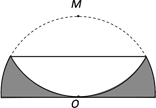
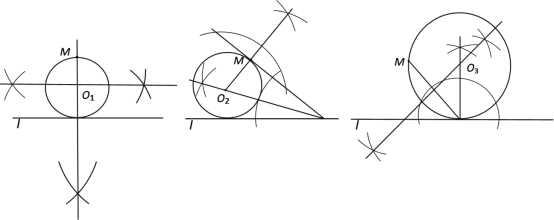
£®1£©»ÁÕº¢Ÿ£¨“—÷™µ„M∫Õ÷±œþl£¨”√¡Ω÷÷≤ªÕ¨µƒ∑Ω∑®ÕÍ≥…≥þπÊ◊˜Õº£∫«Û◊˜°—O£¨ π°—Oπ˝Mµ„£¨«“”Î÷±œþlœý«–£Æ£®√ø÷÷∑Ω∑®◊˜≥ˆ“ª∏ˆ‘≤º¥ø…£¨±£¡Ù◊˜Õº∫€º££¨≤ª–¥◊˜∑®£©

£®Œ Ã‚Ω‚æˆ£©
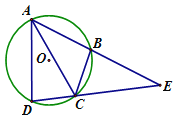
»ÁÕº¢⁄£¨‘⁄Rt°˜ABC÷–£¨°œC£Ω90°„£¨AC£Ω8£¨BC£Ω6£Æ
£®2£©“—÷™°—Oæ≠π˝µ„C£¨«“”Î÷±œþABœý«–£Æ»Ù‘≤–ƒO‘⁄°˜ABCµƒƒ⁄≤ø£¨‘Ú°—O∞Îæ∂rµƒ»°÷µ∑∂ŒßŒ™ £Æ
£®3£©µ„D «±þAB…œ“ªµ„£¨BD£Ωm£¨«Î÷±Ω”–¥≥ˆ±þAC…œ πµ√°œBEDŒ™÷±Ω« ±µ„Eµƒ∏ˆ ˝º∞œý”¶µƒmµƒ»°÷µ∑∂Œß£Æ

°æ¥∞∏°ø£®1£©º˚Ω‚Œˆ£ª£®2£©![]() £ª£®3£©º˚Ω‚Œˆ.
£ª£®3£©º˚Ω‚Œˆ.
°æΩ‚Œˆ°ø
(1)π˝÷±œþÕ‚“ªµ„◊˜“—÷™÷±œþµƒ¥πœþ£¨◊˜œþ∂Œµƒ¥π÷±∆Ω∑÷œþ»∑∂®‘≤–ƒ£¨¥”∂¯ª≠‘≤£ª
(2)∑÷±◊˜≥ˆ∑˚∫œÃ‚“‚µƒ¡ŸΩÁµ„Õº–Œ£¨»∑∂®∞Îæ∂µƒ»°÷µ∑∂Œß;
(3)∏˘æð‘≤÷ÐΩ«∂®¿Ì£¨µ„E‘⁄“‘BCŒ™÷±æ∂µƒ‘≤…œ£¨¥”∂¯»∑∂®≥ˆ∑˚∫œÃıº˛µƒ‘≤µƒ∞Îæ∂µƒ»°÷µ∑∂Œß.
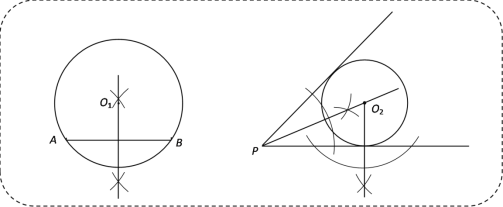
£®1£©»ÁÕº£¨
£®2£©»ÁÕº£∫
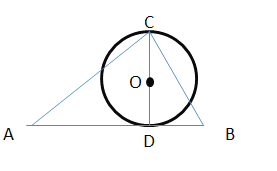
¥À ±‘≤Oµƒ∞Îæ∂◊Ó–°£¨°þ‘≤O”ÎABœý«–£¨
°ýCD°ÕAB£¨∏˘æð÷±Ω«»˝Ω«–Œµƒ√ʪ˝π´ Ωø…µ√£∫
![]()
∏˘æðπ¥π…∂®¿Ìø…µ√£∫![]()
°ý10CD=8°¡6
CD=4.8£¨º¥¥À ±‘≤µƒ∞Îæ∂r=2.4

»ÁÕº£¨µ±‘≤–ƒO‘⁄AC±þ…œ ±£¨∏˘æð“‚…ËOC=OD=x,‘ÚAO=8-x
°þ°œODA=°œBCA=90°„£¨«“°œA=°œA
°ý°˜AOD°◊°˜ABC
°ý![]() ,
,![]() Ω‚µ√x=3
Ω‚µ√x=3
°ý![]()
£®3£©»ÁÕº£∫
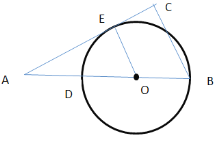
∏˘æð‘≤÷ÐΩ«∂®¿Ì°œBEDŒ™÷±Ω« ±£¨‘Ú“‘BDŒ™÷±æ∂µƒ‘≤”ÎACΩª”⁄µ„E£¨µ±OE°ÕAC ±£¨¥À ±”–“ª∏ˆµ„E∑˚∫œÃıº˛£¨”…“‚ø…÷™£∫OE=![]() £¨AO=
£¨AO=![]()
°þOE°ŒBC
°ý![]() ,
, 
Ω‚µ√£∫m=7.5
µ±BD=AB ±£¨µ„E”ε„C÷ÿ∫œ£¨¥À ±m=10
°ý![]() ±£¨”–1∏ˆµ„E∑˚∫œÃ‚“‚
±£¨”–1∏ˆµ„E∑˚∫œÃ‚“‚
![]() ±£¨”–0∏ˆµ„E∑˚∫œÃ‚“‚
±£¨”–0∏ˆµ„E∑˚∫œÃ‚“‚
![]() ±£¨”–2∏ˆµ„E∑˚∫œÃ‚“‚.
±£¨”–2∏ˆµ„E∑˚∫œÃ‚“‚.

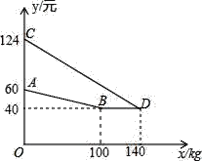
°æƒø°øƒ≥≤˙∆∑√øº˛≥…±æŒ™20‘™£¨æ≠π˝ –≥°µ˜—–∑¢œ÷£¨’‚÷÷≤˙∆∑‘⁄Œ¥¿¥20Ãσ⁄µƒ»’œ˙ €¡ø![]() £®µ•Œª£∫º˛£© «πÿ”⁄ ±º‰
£®µ•Œª£∫º˛£© «πÿ”⁄ ±º‰![]() £®µ•Œª£∫ÃÏ£©µƒ“ª¥Œ∫Ø ˝£¨µ˜—–À˘ªÒµƒ≤ø∑÷ ˝æð»Áœ¬±Ì£∫
£®µ•Œª£∫ÃÏ£©µƒ“ª¥Œ∫Ø ˝£¨µ˜—–À˘ªÒµƒ≤ø∑÷ ˝æð»Áœ¬±Ì£∫
±º‰ | 1 | 3 | 10 | 20 |
»’œ˙ €¡ø | 98 | 94 | 80 | 60 |
’‚20ÃÏ÷–£¨∏√≤˙∆∑√øÃϵƒº€∏Ò![]() £®µ•Œª£∫‘™/º˛£©”Î ±º‰
£®µ•Œª£∫‘™/º˛£©”Î ±º‰![]() µƒ∫Ø ˝πÿœµ ΩŒ™£∫
µƒ∫Ø ˝πÿœµ ΩŒ™£∫![]() £®
£®![]() Œ™’˚ ˝£©£¨∏˘æð“‘…œÃ·π©µƒÃıº˛Ω‚戜¬¡–Œ £∫
Œ™’˚ ˝£©£¨∏˘æð“‘…œÃ·π©µƒÃıº˛Ω‚戜¬¡–Œ £∫
£®1£©÷±Ω”–¥≥ˆ![]() πÿ”⁄
πÿ”⁄![]() µƒ∫Ø ˝πÿœµ Ω£ª
µƒ∫Ø ˝πÿœµ Ω£ª
£®2£©’‚20ÃÏ÷–ƒƒ“ªÃϵƒ»’œ˙ €¿˚»Û◊Ó¥Û£¨◊Ó¥Ûµƒœ˙ €¿˚»Û «∂ý…Ÿ£ø
£®3£©‘⁄ µº œ˙ €µƒ20ÃÏ÷–£¨√øœ˙ €“ªº˛…Ã∆∑æÕæË‘˘![]() ‘™£®
‘™£®![]() £©∏¯œ£Õ˚π§≥ã¨Õ®π˝œ˙ €º«¬º∑¢œ÷£¨’‚20ÃÏ÷–£¨√øÃÏø€≥˝æË‘˘∫Ûµƒ»’œ˙¿˚»ÛÀÊ ±º‰
£©∏¯œ£Õ˚π§≥ã¨Õ®π˝œ˙ €º«¬º∑¢œ÷£¨’‚20ÃÏ÷–£¨√øÃÏø€≥˝æË‘˘∫Ûµƒ»’œ˙¿˚»ÛÀÊ ±º‰![]() µƒ‘ˆ¥Û∂¯‘ˆ¥Û£¨«Û
µƒ‘ˆ¥Û∂¯‘ˆ¥Û£¨«Û![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.