题目内容
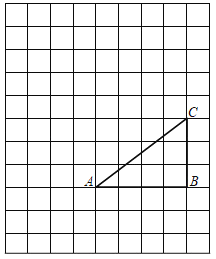
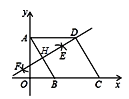
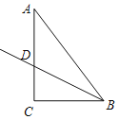
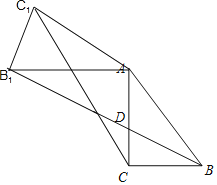
【题目】如图,已知△ABC中,∠C=90°,BC=3,AC=4,BD平分∠ABC,将△ABC绕着点A旋转后,点B、C的对应点分别记为B1、C1,如果点B1落在射线BD上,那么CC1的长度为_____.
【答案】![]()
【解析】
先根据勾股定理求得AB的长,再根据旋转的性质推出AB1∥BC,进而可得△AB1D∽△CBD,然后根据相似三角形的性质求出AD、CD的长,于是![]() 可求,再利用△ACC1∽△ABB1即可求出结果.
可求,再利用△ACC1∽△ABB1即可求出结果.
解:∵∠C=90°,BC=3,AC=4,∴AB=5,
∵将△ABC绕着点A旋转后得△AB1C1,
∴AC1=AC=4,AB1=AB=5,∠CAC1=∠BAB1,
∴∠AB1B=∠ABB1,
∵BD平分∠ABC,∴∠ABB1=∠CBB1,
∴∠AB1B=∠CBB1,
∴AB1∥BC,
∴∠B1AC=∠ACB=90°,∴△AB1D∽△CBD,
∴![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
∵∠C1AC=∠B1AB,AC=AC1,AB=AB1,∴△ACC1∽△ABB1,
∴![]() ,∴
,∴![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目