ΧβΡΩΡΎ»ί
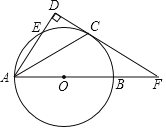
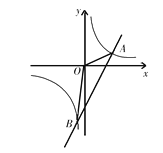
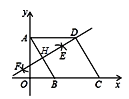
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏyΘΫax2+bx+4Θ®aΓΌ0Θ©”κx÷αΫΜ”ΎAΘ®©¹3Θ§0Θ©Θ§C Θ®4Θ§0Θ©ΝΫΒψΘ§”κy÷αΫΜ”ΎΒψBΘ°
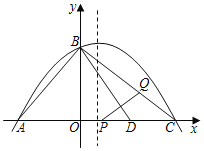
Θ®1Θ©«σ’βΧθ≈ΉΈοœΏΒΡΕΞΒψΉχ±ξΘΜ
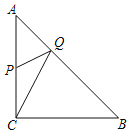
Θ®2Θ©“―÷ΣADΘΫABΘ®ΒψD‘ΎœΏΕΈAC…œΘ©Θ§”–“ΜΕ·ΒψP¥”ΒψA―ΊœΏΕΈAC“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»“ΤΕ·ΘΜΆ§ ±Νμ“ΜΗωΒψQ“‘Ρ≥“ΜΥΌΕ»¥”ΒψB―ΊœΏΕΈBC“ΤΕ·Θ§Ψ≠ΙΐtΘ®sΘ©ΒΡ“ΤΕ·Θ§œΏΕΈPQ±ΜBD¥Ι÷±ΤΫΖ÷Θ§«σtΒΡ÷ΒΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡ«ιΩωœ¬Θ§≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œ «Ζώ¥φ‘Ύ“ΜΒψMΘ§ ΙMQ+MCΒΡ÷ΒΉν–ΓΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΒψMΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©’βΧθ≈ΉΈοœΏΒΡΕΞΒψΉχ±ξ «Θ®![]() Θ§
Θ§![]() Θ©ΘΜΘ®2Θ©tΘΫ
Θ©ΘΜΘ®2Θ©tΘΫ![]() ΘΜΘ®3Θ©¥φ‘ΎΘ§MΘ®
ΘΜΘ®3Θ©¥φ‘ΎΘ§MΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί≈ΉΈοœΏΆΦœώ…œΒΡ»ΐΒψΉχ±ξΘ§άϊ”Ο¥ΐΕ®œΒ ΐΖ®Φ¥Ω…Ϋβ¥πΘΜ
Θ®2Θ©ΗυΨίAΓΔBΒΡΉχ±ξΘ§“Ή«σΒΟAD=AB=5Θ§‘ρCD=AC-AD=2Θ§Ν§Ϋ”DQΘ§”…”ΎBD¥Ι÷±ΤΫΖ÷PQΘ§Ρ«Ο¥DP=DQΘ§ΗυΨίΒ»―ϋ»ΐΫ«–Έ»ΐœΏΚœ“ΜΒΡ–‘÷ ÷ΣΘΚΓœPDB=ΓœQDB=ΓœABDΘ§Φ¥AB//DQΘ§¥Υ ±ΓςCDQΓΉΓςCABΘ§άϊ”ΟœύΥΤ»ΐΫ«–ΈΒΟΒΫΒΡ±»άΐœΏΕΈΦ¥Ω…«σΒΟD QΓΔPDΒΡ≥ΛΘ§¥”Εχ«σΒΟAPΒΡ÷ΒΘ§Φ¥Ω…«σΒΟtΒΡ÷ΒΘΜ
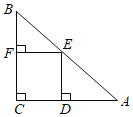
Θ®3Θ©»γΆΦ2Θ§œ»ΉςCΙΊ”ΎΕ‘≥Τ÷αΒΡΕ‘≥ΤΒψΘ§Φ¥ΒψAΘΜΝ§Ϋ”AQ”κΕ‘≥Τ÷αΒΡΫΜΒψΨΆ «Υυ«σΒΡMΘ§œ»«σ2ΒΡΉχ±ξΘ§«σ÷±œΏ42ΒΡΫβΈω ΫΘ§“ρΈΣΕ‘≥Τ÷α «ΘΚx=![]() Θ§Φ¥MΒΡΚαΉχ±ξΨΆ «
Θ§Φ¥MΒΡΚαΉχ±ξΨΆ «![]() Θ§¥ζ»κAQΒΡΫβΈω Ϋ«σ≥ωyΒΡ÷ΒΘ°
Θ§¥ζ»κAQΒΡΫβΈω Ϋ«σ≥ωyΒΡ÷ΒΘ°
ΫβΘΚΘ®1Θ©ΓΏ≈ΉΈοœΏyΘΫax2+bx+4Θ®aΓΌ0Θ©”κx÷αΫΜ”ΎAΘ®©¹3Θ§0Θ©Θ§C Θ®4Θ§0Θ©ΝΫΒψΘ§
Γύ![]() Θ°
Θ°
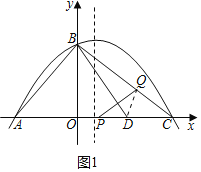
Ϋβ’βΗωΖΫ≥ΧΘ§ΒΟ
ΓύΗΟ≈ΉΈοœΏΫβΈω Ϋ «yΘΫ©¹![]() x2+
x2+![]() x+4Θ°
x+4Θ°
ΓΏyΘΫ©¹![]() x2+
x2+![]() x+4ΘΫyΘΫ©¹
x+4ΘΫyΘΫ©¹![]() Θ®x©¹
Θ®x©¹![]() Θ©2+
Θ©2+![]() Θ°
Θ°
Γύ’βΧθ≈ΉΈοœΏΒΡΕΞΒψΉχ±ξ «Θ®![]() Θ§
Θ§![]() Θ©ΘΜ
Θ©ΘΜ
Θ®2Θ©ΓΏAΘ®©¹3Θ§0Θ©Θ§C Θ®4Θ§0Θ©Θ§
ΓύOAΘΫ3Θ§OBΘΫOCΘΫ4Θ§
‘ρABΘΫ5Θ§ACΘΫ7Θ§CDΘΫ2ΘΜ
»γΆΦ1Θ§Ν§Ϋ”DQΘ§”…”ΎBD¥Ι÷±ΤΫΖ÷PQΘ§‘ρDPΘΫDQΘ§ΒΟΘΚ
ΓœPDBΘΫΓœQDBΘ§
ΕχADΘΫABΘ§ΒΟΘΚΓœABDΘΫΓœADBΘ§
Ι ΓœQDBΘΫΓœABDΘ§
ΒΟQDΓΈABΘΜ
ΓύΓςCDQΓΉΓςCABΘ§‘ρ”–ΘΚ![]() ΘΫ
ΘΫ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
Γύ![]() ΘΫ
ΘΫ![]() Θ°
Θ°
ΓύPDΘΫDQΘΫ![]() Θ§APΘΫAD©¹PDΘΫ5©¹
Θ§APΘΫAD©¹PDΘΫ5©¹![]() ΘΫ
ΘΫ![]() Θ§
Θ§
Ι tΘΫ![]() ΘΜ
ΘΜ
Θ®3Θ©¥φ‘ΎΘ§
»γΆΦ2Θ§Ν§Ϋ”AQΫΜΕ‘≥Τ÷α”ΎMΘ§¥Υ ±MQ+MCΈΣΉν–ΓΘ§
ΙΐQΉςQNΓΆx÷α”ΎNΘ§
ÿDQøABȧ
ΓύΓœQDNΘΫΓœBACΘ§
sinΓœQDNΘΫsinΓœBACΘΫ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
Γύ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΓύQNΘΫ![]() Θ§
Θ§
…η÷±œΏBCΒΡΫβΈω ΫΈΣΘΚyΘΫkx+bΘ§
Α―BΘ®0Θ§4Θ©ΚΆCΘ®4Θ§0Θ©¥ζ»κΒΟΘΚ![]() Θ§
Θ§
ΫβΒΟ![]() Θ§
Θ§
Γύ÷±œΏBCΒΡΫβΈω ΫΈΣΘΚyΘΫ©¹x+4Θ§
Β±yΘΫ![]() ±Θ§
±Θ§![]() ΘΫ©¹x+4Θ§
ΘΫ©¹x+4Θ§
xΘΫ![]() Θ§
Θ§
ΓύQΘ®![]() Θ§
Θ§![]() Θ©Θ§
Θ©Θ§
Ά§άμΩ…ΒΟΘΚAQΒΡΫβΈω ΫΈΣΘΚyΘΫ![]() x+
x+![]() Θ§
Θ§
Β±xΘΫ![]() ±Θ§yΘΫ
±Θ§yΘΫ![]() ΓΝ
ΓΝ![]()
![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΓύMΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°


ΓΨΧβΡΩΓΩΡ≥≥§ –ΦΤΜ°ΙΚΫχΦΉΓΔ““ΝΫ÷÷…ΧΤΖΘ§ΝΫ÷÷…ΧΤΖΒΡΫχΦέΓΔ έΦέ»γœ¬±μΘΚ
…ΧΤΖ | ΦΉ | ““ |
ΫχΦέΘ®‘Σ/ΦΰΘ© |
|
|
έΦέΘ®‘Σ/ΦΰΘ© | 200 | 100 |
»τ”Ο360‘ΣΙΚΫχΦΉ÷÷…ΧΤΖΒΡΦΰ ΐ”κ”Ο180‘ΣΙΚΫχ““÷÷…ΧΤΖΒΡΦΰ ΐœύΆ§Θ°
Θ®1Θ©«σΦΉΓΔ““ΝΫ÷÷…ΧΤΖΒΡΫχΦέ «Εύ…Ό‘ΣΘΩ
Θ®2Θ©»τ≥§ –œζ έΦΉΓΔ““ΝΫ÷÷…ΧΤΖΙ≤50ΦΰΘ§Τδ÷–œζ έΦΉ÷÷…ΧΤΖΈΣ![]() ΦΰΘ®
ΦΰΘ®![]() Θ©Θ§…ηœζ έΆξ50ΦΰΦΉΓΔ““ΝΫ÷÷…ΧΤΖΒΡΉήάϊ»σΈΣ
Θ©Θ§…ηœζ έΆξ50ΦΰΦΉΓΔ““ΝΫ÷÷…ΧΤΖΒΡΉήάϊ»σΈΣ![]() ‘ΣΘ§«σ
‘ΣΘ§«σ![]() ”κ
”κ![]() ÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ω
÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ω![]() ΒΡΉν–Γ÷ΒΘ°
ΒΡΉν–Γ÷ΒΘ°