题目内容
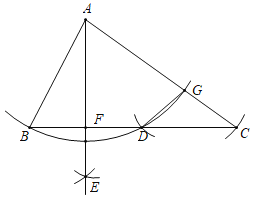
【题目】如图,在△ABC中,∠B=2∠C,以点A为圆心,AB长为半径作弧,交BC于点D,交AC于点G;再分别以点B和点D为圆心,大于![]() BD的长为半径作弧,两弧相交于点E,作射线AE交BC于点F,若以点G为圆心,GC长为半径作两段弧,一段弧过点C,而另一段弧恰好经过点D,则此时∠FAC的度数为( )
BD的长为半径作弧,两弧相交于点E,作射线AE交BC于点F,若以点G为圆心,GC长为半径作两段弧,一段弧过点C,而另一段弧恰好经过点D,则此时∠FAC的度数为( )
A.54°B.60°C.66°D.72°
【答案】A
【解析】
连接AD,根据作图过程可得,AE是BD的垂直平分线,DG=CG,AB=AD=AG,设∠C=x,则∠CDG=x,∠AGD=2x,根据∠ADB+∠ADG+∠GDC=2x+2x+x=180°,求出x的值后再根据直角三角形两个锐角互余即可求得∠FAC的度数.
解:如图,连接AD,
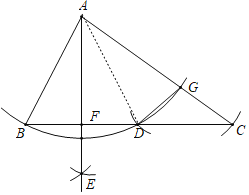
根据作图过程可知:
AE是BD的垂直平分线,DG=CG,AB=AD=AG,
设∠C=x,则∠CDG=x,∠AGD=2x,
∴∠ADG=∠AGD=2x,
∵∠B=2∠C,
∴∠B=2x,
∴∠ADB+∠ADG+∠GDC=2x+2x+x=180°,
∴x=36°,
∴∠FAC=90°﹣36°=54°.
故选:A.

练习册系列答案
相关题目
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) |
|
|
售价(元/件) | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共50件,其中销售甲种商品为![]() 件(
件(![]() ),设销售完50件甲、乙两种商品的总利润为
),设销售完50件甲、乙两种商品的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最小值.
的最小值.