��Ŀ����
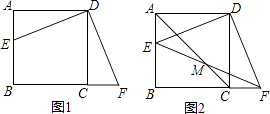
����Ŀ����֪����ͼ1�������Ϊ3��������ABCD�У�E��F�ֱ���BC��CD���ϵ����㣬AE��BF�ڵ�G����BE=1��
��1����֤����ABE�ա�BCF��
��2�������ABE����BCF�ص����֣�����BEG���������
��3���ֽ���ABE�Ƶ�A��ʱ�뷽����ת����AB��E������ͼ2����ʹ��E����CD���ϵĵ�E����������ABE����תǰ������BCF�ص����ֵ�����Ƿ����˱仯����˵�����ɣ�
���𰸡���1��֤����������
��2��![]() ��
��
��3��û�б仯�����ɼ�����.
�������������������1�����ı���ABCD�������Σ��ɵ���ABE=��BCF=90����AB=BC������AE��BF����ͬ�ǵ������ȣ�����֤����BAE=��CBF��Ȼ������ASA�������ж�����ABE�ա�BCF��
��2����������ABCD���������3��������ô������εı߳���������BGE����ABE�У���GBE=��BAE����EGB=��EBA=90������֤����BGE�ס�ABE�������������ε�����ȵ������Ʊȵ�ƽ����������ô𰸣�
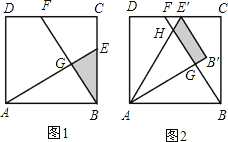
��3�����������к����������BAE=30������֤��Rt��ABE��Rt��AB��E���Rt��ADE�����ɵ�DE��=B��E��=BE���ɣ�1����֪BE=CF���Ӷ���CF=DE�����̶��ɵ�DF=CE����
�����������1��������ABCD�У�AB=BC����ABC=��BCF=90�������ABF+��CBF=90���� ��AE��BF�� ���ABF+��BAE=90�������CBF=��BAE �����ABE �ա�BCF ��
��2�������������Ϊ3����AB=![]() ���ߡ�GBE=��BAE����EGB=��EBA=90�������BGE�ס�ABE����
���ߡ�GBE=��BAE����EGB=��EBA=90�������BGE�ס�ABE����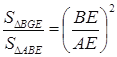 ������BE=1����AE2=AB2+BE2=3+1=4����S��BGE=
������BE=1����AE2=AB2+BE2=3+1=4����S��BGE=![]() =
=![]() ��
��
��3�� ��BE=1��AB=![]() ����tan��BAE=
����tan��BAE=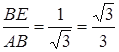 �����BAE=30��������֪��֤��Rt��ABE��Rt��AB��E���Rt��ADE������DE��=B��E��=BE���ߡ�ABE�ա�BCF����BE=CF����CF=DE������DF=CE����
�����BAE=30��������֪��֤��Rt��ABE��Rt��AB��E���Rt��ADE������DE��=B��E��=BE���ߡ�ABE�ա�BCF����BE=CF����CF=DE������DF=CE����

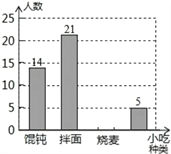
 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д� ���������ν�ϵ�д�
���������ν�ϵ�д�