Question

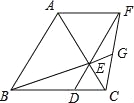
【题目】如图，在锐角三角形ABC中，点D、E分别在边AC、AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF＝∠GAC．

（1）求证：△ADE∽△ABC；

（2）若AD＝BE＝4，AE＝3，求CD的值．

Answer 1

【答案】(1)详见解析;(2)

【解析】

(1)由∠EAF=∠GAC.可得∠EAG=∠DAF且AG⊥BC，AM⊥DE 可得∠ADF=∠B，且∠EAD=∠BAC可证：△ADE∽△ABC；

（2）利用相似的性质得出，AB＝BE+AE＝4+3＝7，即可解答

（1）证明：AG⊥BC，AF⊥DE，

∴∠AFE＝∠AGC＝90°，

∴∠AEF+∠EAF＝90°，∠GAC+∠ACG＝90°，

∵∠EAF＝∠GAC，

∴∠AEF＝∠ACG，

∵∠EAD＝∠CAB，

∴△ADE∽△ABC；

（2）解：∵△ADE∽△ABC，

∴，

∵AD＝BE＝4，AE＝3，

∴AB＝BE+AE＝4+3＝7，

∴，

解得：AC＝ ，

∴CD＝AC﹣AD＝﹣4＝ ．