题目内容
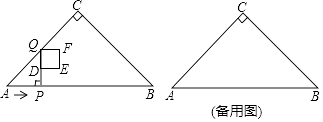
【题目】一幢房屋的侧面外墙壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°,外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG∥EH,GH=2.6m,∠FGB=65°.
(1)求证:GF⊥OC;
(2)求EF的长(结果精确到0.1m).
(参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91)
【答案】
(1)证明:CD与FG交于点M,
∵∠OCD=25°,四边形ABCD是矩形,∠FGB=65°.
∴∠FMC=65°,
∴∠MFC=90°,
∴GF⊥CO
(2)解:作GN⊥EH于点N,

∵FG∥EH,GF⊥CO;
∴四边形ENGF是矩形;
∴EF=NG,
∵∠FGB=∠NHG=65°,
∴sin65°= ![]() =
= ![]() ≈0.91,
≈0.91,
∴EF=NG=2.366m≈2.4m.
【解析】(1)利用矩形的性质和已知易证;
(2)作GN⊥EH于点N,易证四边形ENGF是矩形,可得EF=NG,在Rt△HGN中利用三角函数可求得NG,即可得到答案.
【考点精析】本题主要考查了平行线的性质和等腰三角形的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.

练习册系列答案
相关题目