题目内容
【题目】已知k为实数,关于x的方程为x2﹣2(k+1)x+k2=0.
(1)请判断x=﹣1是否可为此方程的根,说明理由.
(2)设方程的两实根为x1,x2,当2x1+2x2+1=x1x2时,试求k的值.
【答案】(1)x=﹣1不是此方程的根;(2)k=5.
【解析】
(1) 当x=-1时, 方程左边=![]() =
=![]() ≠0, 右边=0≠左边, 得出x=-1不是此方程的根;
≠0, 右边=0≠左边, 得出x=-1不是此方程的根;
(2)由根与系数的关系得:![]() ,
,![]() , 由已知得出方程, 解方程即可.
, 由已知得出方程, 解方程即可.
解:(1)x=﹣1不是此方程的解;理由如下:
当x=﹣1时,方程左边=1+2(k+1)+k2=(k+1)2+2≠0,右边=0≠左边,
∴x=﹣1不是此方程的根;
(2)由根与系数的关系得:x1+x2=2(k+1),x1x2=k2,
∵2x1+2x2+1=x1x2,
∴4(k+1)+1=k2,
解得:k=﹣1(方程无实根,舍去),或k=5,
∴k=5.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图,试根据以上提供的信息解答下列问题:
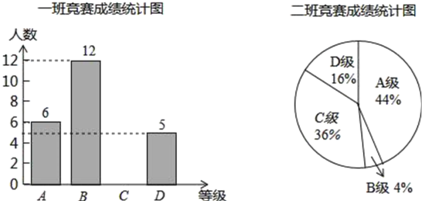
(1)把一班竞赛成绩统计图补充完整;
(2)根据下表填空:a= ,b= ,c= ;
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | 87.6 | 80 | c |
(3)请从平均数和中位数或众数中任选两个对这次竞赛成绩的结果进行分析.