题目内容
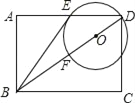
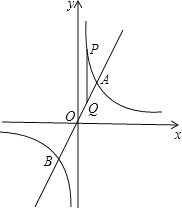
【题目】如图,已知直线y=kx(k>0)与双曲线![]() 交于A、B两点,且点A的纵坐标为4,第一象限的双曲线上有一点
交于A、B两点,且点A的纵坐标为4,第一象限的双曲线上有一点![]() ,过点P作PQ//y轴交直线AB于点Q.
,过点P作PQ//y轴交直线AB于点Q.
(1)直接写出k的值及点B的坐标:
(2)求线段PQ的长;
(3)如果在直线y=kx上有一点M,且满足△BPM的面积等于12,求点M的坐标.
【答案】(1)![]() ;(2)6;(3)点M的坐标
;(2)6;(3)点M的坐标![]() 或
或![]()
【解析】
(1)先求得A点坐标,再代入直线解析式可求得k的值,根据对称性可求得B点坐标;
(2)由反比例函数解析式可求得P点坐标,由直线解析式可求得Q点坐标,可求得PQ的长;
(3)可设M坐标为(m,2m),分点M在线段BQ的延长线上和线段QB的延长线上两种情况,分别表示出△BPM的面积,可求得m的值,可求得M的坐标.
解:(1)∵A在双曲线![]() 上,且A的纵坐标为4,
上,且A的纵坐标为4,
∴A坐标为(2,4),
代入直线y=kx,可得4=2k,解得k=2,
又A、B关于原点对称,
∴点B的坐标为(-2,-4).
(2)∵点P(1,a)在双曲线上,
∴代入![]() ,可得点P的坐标为(1,8).
,可得点P的坐标为(1,8).
∵PQ∥y轴,且点Q在直线AB上,
∴可设点Q的坐标为(1,b).
代入y=2x,得点Q的坐标为(1,2).
∴PQ=6.
(3)设点M的坐标为(m,2m).
![]()
①当点M在BQ的延长线上时,S△BPM=S△BPQ+S△MPQ,![]()
点M的坐标为(2,4).
②当点M在QB的延长线上时,S△BPM=S△MPQ-S△BPQ,![]()
点M的坐标为(-6,-12).
综上所述:点M的坐标为(2,4),(-6,-12).

【题目】今年5月19日为第29个“全国助残日”我市某中学组织了献爱心捐款活动,该校数学课外活动小组对本次捐款活动做了一次抽样调查,并绘制了如下不完整的频数分布表和频数分布直方图(每组含前一个边界,不含后一个边界).
捐款额(元) | 频数 | 百分比 |
| 3 | 7.5% |
| 7 | 17.5% |
| a | b |
| 10 | 25% |
| 6 | 15% |
总计 | 100% |
(1)填空:![]() ________,
________,![]() ________.
________.
(2)补全频数分布直方图.
(3)该校有2000名学生估计这次活动中爱心捐款额在![]() 的学生人数.
的学生人数.