题目内容
【题目】在等腰三角形ABC中，AB＝AC＝10，BC＝12，D为BC边上的任意一点，过点D分别作DE⊥AB，DF⊥AC，垂足分别为E，F，则DE＋DF＝______．
【答案】9.6
【解析】分析：如图连接AD，作AH⊥BC于H．首先利用勾股定理求出AH，再根据S△ABC=S△ABD+S△ACD，DE⊥AB，DF⊥AC，可得
BCAH=ABDE+ACDF，由此即可解决问题．
详解：如图，连接AD，作AH⊥BC于H．
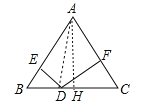
∵AB=AC=10，AH⊥BC，∴BH=CH=6．在Rt△ABH中，AH=
=
=8．
∵S△ABC=S△ABD+S△ACD，DE⊥AB，DF⊥AC，∴BCAH=ABDE+ACDF，∴6×8=5DE+5DF，∴DE+DF=9.6．
故答案为：9.6．
练习册系列答案
相关题目
