Question

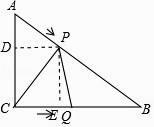
【题目】已知：Rt△ABC中，∠ACB=90°，CA=3，CB=4，设P，Q分别为AB边，CB边上的动点，它们同时分别从A，C出发，以每秒1个单位长度的速度向终点B运动，设P，Q运动的时间为t秒．

（1）求△CPQ的面积S与运动时间t之间的函数关系式，并求出S的最大值．
（2）t为何值时，△CPQ为直角三角形．
（3）①探索：△CPQ是否可能为正三角形，说明理由．
②P，Q两点同时出发，若点P的运动速度不变，试改变点Q的运动速度，使△CPQ为正三角形，求出点Q的运动速度和此时的t值．

Answer 1

【答案】
（1）

解：作PD⊥AC于D，PE⊥BC于E，

∵∠ACB=90°，CA=3，CB=4，

∴AB= =5，

∵AP=t，

∴AD= t，PD= t，

∴PE=DC=3﹣ t，

∴S= ×t×（3﹣ t）=﹣ t2+ t，

∵S=﹣ t2+ t=﹣ （t﹣ ）2+ ，

∴S的最大值为 ；

（2）

解：只有当PC2+PQ2=CQ2时，△CPQ为直角三角形，

∴（ t）2+（3﹣ t）2+（3﹣ t）2+（t﹣ t）2=t2，

解得，t1=3，t2=15（舍去），

∴当t=3时，△CPQ为直角三角形；

（3）

①△CPQ不可能为正三角形，

理由如下：若△CPQ是正三角形，

则PC=PQ，EC=EQ，即t﹣ t= t，

解得，t=0，

∴△CPQ不可能为正三角形；

②设点Q的运动速度为a，

当CE=EQ时，即 t=at﹣ t，

解得，a= ，

∵∠PCQ=60°，

∴PE= PD，

解得，t= ．

【解析】（1）作PD⊥AC于D，PE⊥BC于E，根据勾股定理求出AB，用t表示出AD、PD，根据三角形的面积公式计算即可；（2）根据勾股定理列出算式，求出t的值；（3）①根据等边三角形的三线合一列式计算即可；②设点Q的运动速度为a，根据等边三角形的性质列式求出a，根据等边三角形的性质、正切的概念计算即可．
【考点精析】通过灵活运用等边三角形的性质和勾股定理的概念，掌握等边三角形的三个角都相等并且每个角都是60°；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题．